4.6 Operační zesilovač

Operační zesilovač byl původně používán jako základní jednotka analogových počítačů, diferenciálních analyzátorů. V posledních letech s rozvojem hybridních a později monolitických integrovaných obvodů se stal operační zesilovač samostatnou jednotkou, elektronickým prvkem. Operační zesilovač používaný ve fyzikálním měření nemusí být ovšem pouze v monolitické formě, ale může být buď v hybridní formě nebo dokonce sestaven z diskrétních prvků.

Vedle použití operačních zesilovačů v analogových počítačích, kde byl hlavně používán pro základní aritmetické operace sečítání, odečítání, dělení a násobení a rovněž pro integraci analogových signálů, se dnes používá i v řadě elektronických obvodů jako jsou stejnosměrné i střídavé zesilovače, komparátory, elektronický vzorkovací obvod (vrátka, gate), klopné obvody, aktivní filtry, převodníky z analogového signálu na číselnou hodnotu a naopak.

V této kapitole vzhledem k všestrannému použití operačních zesilovačů budou podány jeho základní vlastnosti s ohledem na jeho možné fyzikální aplikace.

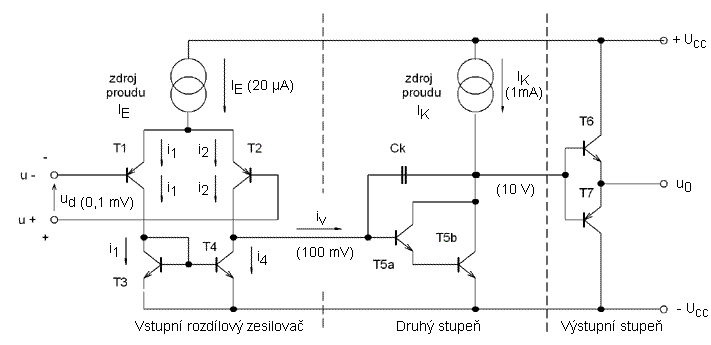
Velmi zjednodušené schéma operačního zesilovače je na obrázku 68. První, velmi důležitou částí operačního zesilovače je vstupní rozdílový zesilovač. Musí zesílit rozdílové napětí u_d 1000 až 10000 krát. Další částí je druhý stupeň tvořený tranzistory T5a, T5b v Darlingtonově zapojení. Vstupní proud této kombinace je velmi malý a neovlivňuje proto vlastnosti rozdílového zesilovače (nezatěžuje jej). Napěťové zesílení je 100 až 300, protože se jedná o  zapojení zesilovače se společným emitorem (a proudovým zdrojem v kolektoru). Kondenzátor C_k (korekční kondenzátor) zamezuje nežádoucím kmitům operačního zesilovače. Může být přímo součástí integrovaného obvodu (operační zesilovač s vnitřní korekcí) nebo se může připojovat jako vnější součástka. Posledním dílem každého operačního zesilovače je výstupní stupeň. Zde jej tvoří komplementární emitorový sledovač (T6, T7), jeho napěťové zesílení je přibližně jednotkové. Výstupní stupeň zabraňuje tomu, aby zatěžovací odpor na výstupu ovlivňoval zesílení druhého stupně - odděluje zátěž od předchozích stupňů s napěťovým zesílením.

Při tak jednoduché konstrukci, jako je na obrázku, můžeme připojit zatěžovací odpory asi 2 kΩ (a větší) a pro napětí u0 = 10 V prochází zatěžovací proud 10 V / 2 kΩ = 5 mA. Předpokládejme, že proudový zesilovací činitel tranzistorů t6 a T7 je alespoň 50. Bázový proud tranzistorů T6 a T7 je potom vždy menší než  než 5 mA / 500 = 100 μA a to je hodnota mnohem menší než proud dodávaný zdrojem proudu I_k. (Zdroj proudu I_k je obvod, který dodává do obvodu stále stejný proud v I_k, bez ohledu na velikost napětí na jeho výstupu). Druhý stupeň proto není zátěží příliš ovlivněn.

Předpokládejme, že proudové zesilovací činitele tranzistorů T5a a T5b jsou stejné a rovny hodnotě 50. Výsledný proudový zesilovací činitel Darlingtonova zapojení je β = 50 . 50 = 2500. Protéká-li kolektorem T5b proud I_k = 1 mA, vtéká do báze tranzistoru T5a proud - 1mA / 2500 = 0,4 μA. to je opět hodnota mnohonásobně menší než je proud proudového zdroje I_E. Druhý stupeň proto podstatně neovlivní zesílení rozdílového stupně.

obr. 68 - Vnitřní zapojení operačního zesilovače

Operační zesilovač má dva vstupní obvody: invertující a neinvertující. Při zavedení signálu na invertující vstup se na výstupu operačního zesilovače objeví signál v opačné fázi, zatímco při přivedení signálu na neinvertující vstup je signál na vstupu a výstupu operačního zesilovače ve fázi.

Zapojení jako invertor:

Inverzní funkci k funkci f můžeme realizovat zapojením nelineárního členu do obvodu zpětné vazby

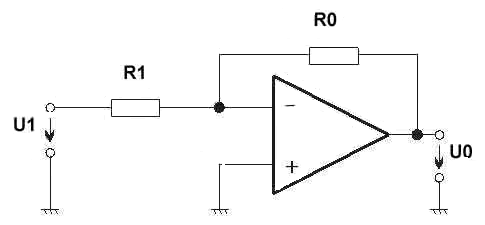
obr. 71 - Invertující zapojení operačního zesilovače

Simulaci tohoto zapojení si můžete stáhnout zde

Chceme-li realizovat logaritmující nebo exponenciální zesilovače, můžeme použít jako nelineárního členu polovodičové diody nebo tranzistoru v tak zvaném diodovém zapojení.

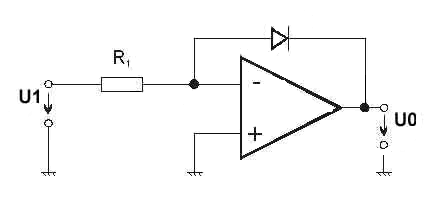
obr. 72 - Diodové zapojení operačního zesilovače

Simulaci tohoto zapojení si můžete stáhnout zde

Pro napětí na diodě je závislost výstupního napětí na napětí vstupním logaritmická.

Zapojení jako integrátor:

Základní zapojení tzv. Millerova integrátoru ukazuje obrázek , pro který lze odvodit operační rovnici pomocí následujících vztahů:

Kde jsou T = RC .......časová konstanta integrátoru

              U_C(t₀) .......napětí na kondenzátoru před začátkem v čase t₀

_{Časová konstanta integrátoru je definována jako doba, za kterou jsou si rovny absolutní hodnoty napětí na vstupu a výstupu integrátoru při skokové změně vstupního napětí (obrázek ). Hodnotu časové konstanty lze měnit při použitém zapojení podle obrázku .princip změny časové konstanty ukazuje obrázek Pro časovou konstantu pak platí vztah:}

_{Nevýhodou integrátoru podle obrázku  je "ujíždění" výstupního napětí integrátoru až do nasycení i při nulovém vstupním napětí, které je způsobeno klidovým vstupním proudem a napěťovou nesymetrií vstupů operačního zesilovače. Proto je nutné vhodným způsobem eliminovat tyto vlivy, případně omezit zesílení integrátoru na velmi nízkých frekvencích paralelním rezistorem Rp ke kondenzátoru. V případě střídavého integrátoru, který zpracovává pouze střídavý signál, je možné eliminovat "ujíždění" integrátoru připojením PI regulátoru stejnosměrné složky, jehož parametry je nutné měnit v závislosti na frekvenci vstupního napětí.}

Na obrázku 73 je vidět nejběžnější zapojení integračního zesilovače. Do obvodu záporné zpětné vazby je připojen kondenzátor. Pro vstupní proud (virtuální zem) platí:

Veškeré proudy tečou do kondenzátoru C. Pro výstupní napětí platí u₀ = - u_c. Pro napětí kondenzátoru C platí:

(102)

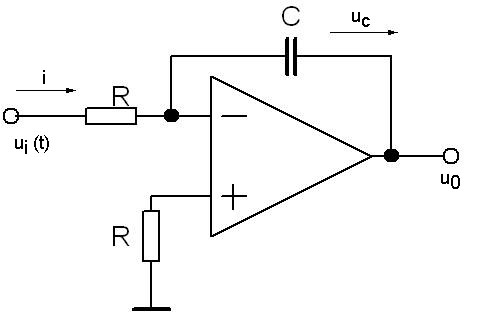obr. 73 - Zapojení integrujícího zesilovače

Průběhy vstupního napětí u0 (t) integrátoru pro: obr. 74 - Průběh vstupního a výstupního napětí když ui (t) = Ui > 0 obr. 75 - Průběh vstupního a výstupního napětí když ui (t) = -Ui < 0

Simulaci tohoto zapojení si můžete stáhnout zde

V praxi je obvykle integrační obvod propojen tak, aby bylo možno zvolit tři pracovní režimy integračního obvodu:

1. Režim nastavení počátečních podmínek (sepnutý kontakt b , rozepnutý kontakt a ).

2. Režim integrace (sepnutý kontakt a , rozepnutý kontakt b ).

3. Režim paměti (režim při rozepnutém kontaktu a i b ).

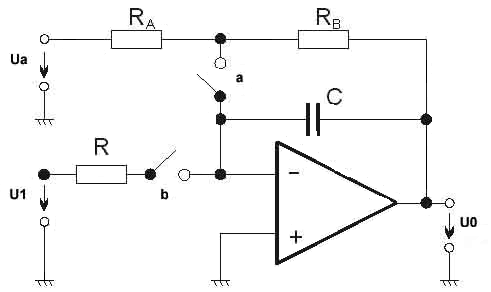
obr. 76 - Praktické zapojení integračního zesilovače

Zapojení jako derivátor:

Derivační zesilovače se používají často při měření vibrací - z derivace lze určit rychlost vibrace. Pomocí derivace lze také odhalit malé (ale rychlé) změny na značných (úrovní), pomalu se měnících signálech - např. zákmity, špičky apod.

Principiální zapojení derivačního zesilovače je zřejmé z obrázku. Pro proud I platí :

(103)

je-li u =0. Potom

(104)

Chování obvodu ve frekvenční oblasti lze snadno určit, že jde o invertující zesilovač se ziskem

(105)

 Zesílení se zvětší na každé zdvojení frekvence dvakrát (+6 dB/okt). Je zřejmé, že zapojení na obrázku zdůrazňuje vyšší kmitočty. Fázový posuv vede k nestabilitě derivačního zesilovače. Tyto problémy lze vyřešit zapojením doplňujících prvků R, C podle obrázku  . Odpor R omezí růst zisku, kondenzátor C dokonce vede k poklesu zisku nad určitý kmitočet (C není nutný, lze využít vlastního poklesu ). Nejčastěji se volí R₁C = RC₁ (oblast kritického úhlového kmitočtu:

(106)

Potom se zapojení chová na nízkých kmitočtech (ω<ω_k)jako derivační zesilovač, na vysokých kmitočtech (ω>ω_k) se chová jako integrační zesilovač.

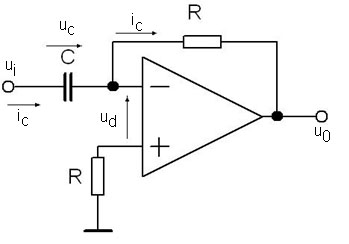obr. 77 - Derivační zesilovač

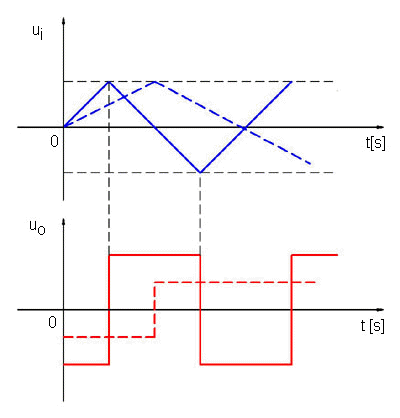obr. 78 - Odezva derivačního zesilovače na vstupní trojúhelníkové napětí; menší strmosti ui odpovídá i menší výstupní napětí

Prakticky se však uvedeného zapojení nepoužívá, neboť derivátor má obrácenou frekvenční charakteristiku než integrátor a při derivování se zesiluje napětí tím více, čím má vyšší frekvenci. Pokud se nelze derivování vyhnout, používá se upravených obvodů, které omezují zesílení na vyšších kmitočtech. Jedním z používaných obvodů je kombinace derivačního a integračního obvodu:

obr. 79 - Reálné zapojení derivačního zesilovače

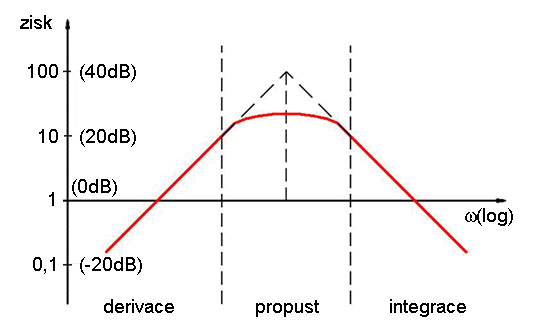
obr. 80 - Závislost přenosu na frekvenci pro reálný derivační zesilovač

Simulaci tohoto zapojení si můžete stáhnout zde

Zapojení jako sumátor:

Součtový invertující zesilovač se třemi vstupy je na obrázku. Počet vstupů lze libovolně zvětšit, mělo by se však brát v potaz, že zbytečné zvyšování počtu vstupů je nevýhodné. Invertující vstup OZ je v tomto zapojení virtuální zemí. Proto platí, že:

Pro ideální OZ platí:

veškeré proudy protékají přes zpětnovazební odpor R. Nyní již lze určit, že

Pro R₁ = R₂ = R₃ = R dostaneme známý vztah

Vstupní odpor pro každý signál u_i je dán odporem R_i (na který je signál přiveden). Všechny vlastnosti jsou stejné jako u invertujícího zesilovače.

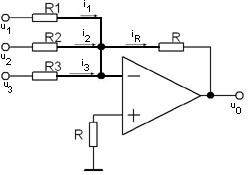
obr. 81 - Součtový invertující zesilovač

Tímto způsobem se realizuje například sčítací nebo odčítací člen ve zpětně vazbě regulačního obvodu.

Zpět