Číslicové zpracování signálů hraje v současné době ve vědě a technice mimořádně důležitou roli. Představuje zpracování číselných posloupností číslicovou technikou. Zpracovávané číslicové posloupnosti mohou být vyrobeny v počítači, ale ve většině případů jsou získány digitalizací (vzorkováním, kvantováním a kódováním) analogového signálu. Tento signál může být jednorozměrný (nejčastěji funkce času) nebo vícerozměrný (nejčastěji dvourozměrný - funkce dvou souřadnic, která vyjadřuje dvourozměrný obraz)
Oblast číslicového zpracování signálů se v posledních desetiletích bouřlivě rozvíjí. Jsou vyvíjeny nové algoritmy a zkoumány jejich chyby. Neustále jsou zlepšovány parametry speciálních polovodičových obvodů určených ke zpracování signálů, tzv. číslicových signálových procesorů.
Důležitým pojmem teorie číslicového zpracování signálů je zpracování signálů v reálném čase. Tímto označením se zpravidla vyjadřuje situace, kdy je celý výpočet algoritmu číslicového zpracování proveden před příchodem dalšího vzorku signálu na vstup bloku blokového schématu, které vyjadřuje zpracování. Musí být tedy čas potřebný k výpočtu algoritmu zpracování kratší než vzorkovací interval. V případech, kdy se zpracovává celý blok dat najednou, jako je to u výpočtů rychlé Fourierovy transformace, se výpočet v reálném čase realizuje tak, že , že FFT spektrální analyzátor má na vstupu dvě paměti, a zatímco se algoritmem FFT zpracovává obsah jedné paměti, plní se druhá paměť. Tím je zajištěno, že že se žádná data pro zpracování neztratí.
Číslicové zpracování signálů se využívá v telekomunikacích, v řídící a měřící technice, při zpracování řeči, v seismologii, radioastronomii, v počítačové grafice, při zpracování obrazů, v lékařství, spotřební elektronice, vojenských aplikacích a dalších oborech. Přitom se využívá známých výhod zpracování signálů v číslicové formě (malá závislost na tolerancích součástek, malá citlivost na rušivé signály, volba přesnosti zpracování délkou slova, programovatelnost použitých obvodů a tím univerzálnost jejich použití).
V měřicí technice se metody zpracování signálů používají zejména při zpracování vzorkovaných dat v moderních číslicových přístrojích (analyzátorech signálů, spektrálních analyzátorech, analyzátorech energie, ale i v některých moderních číslicových multimetrech) a při zpracování vzorkovaných dat na počítačích nebo pomocí číslicových signálových procesorů. Využívají se zejména algoritmy rychlé Fourierovy transformace a číslicové filtrace, které jsou součástí řady programů pro výpočet frekvenčních spekter signálů, výkonových spektrálních hustot, korelačních, kovariančních a koherenčních funkcí apod. Knihovny pro zpracování signálů jsou součástí řady komerčně dostupných programových balíků pro počítače. K úlohám zpracování signálů patří analýza signálů a nalezení různých parametrů signálů, úprava signálů pro získání požadovaných vlastností a generování signálů s požadovanými vlastnostmi.
Moderní analyzátory signálu umožňují měřit řadu funkcí a používají složité algoritmy zpracování signálu. Pokud uživatel vlastnosti a způsob výpočtu měřených funkcí nezná, může výsledky měření interpretovat zcela nesprávně.
Účelem této práce je seznámit čtenáře se základními algoritmy číslicového zpracování signálů a se základními metodami zpracování stacionárních a jednorozměrných stochastických signálů.
Na závěr této úvodní partie uvedu rozdělení signálů.
Z hlediska determiničnosti signály dělíme na signály deterministické a signály náhodné stochastické.
Deterministické signály lze popsat matematickou funkcí, takže umíme určit jejich hodnotu pro libovolnou hodnotu nezávisle proměnné (kterou bývá u jednorozměrných signálů nejčastěji čas).
Patří k nim signály periodické, signály kvaziperiodické a signály přechodné. Podskupinou periodických signálů jsou signály antiperiodické, pro které platí f (t + T /2) = - f (t), takže jejich druhá polovina periody je podle vodorovné osy osově souměrná s první polovinou posunutou o polovinu periody.
Kvaziperiodické signály jsou tvořeny součtem několika harmonických (sinusových) signálů, jejichž frekvence nejsou celistvými násobky jedné základní frekvence. Jejich příkladem jsou amplitudově nebo frekvenčně modulované signály. Přechodné signály trvají omezenou dobu nebo teoreticky neomezenou dobu, ale periodicky se neopakují. Jejich kmitočtové spektrum je spojité. Příkladem jsou průběhy napětí při přechodných dějích v elektrických obvodech.
Náhodné (stochastické) signály lze popisovat pouze statisticky.
Signály dělíme rovněž podle frekvence, a to:
technický střídavý proud - do 100 Hz
nízká frekvence, (nf) - 0 až 20 kHz
vysoká frekvence, (vf) - kilohertzy až megahertzy (kHz až MHz)
nejvyšší frekvence - kolem 1000 megahertzů (1 GHz) a výše

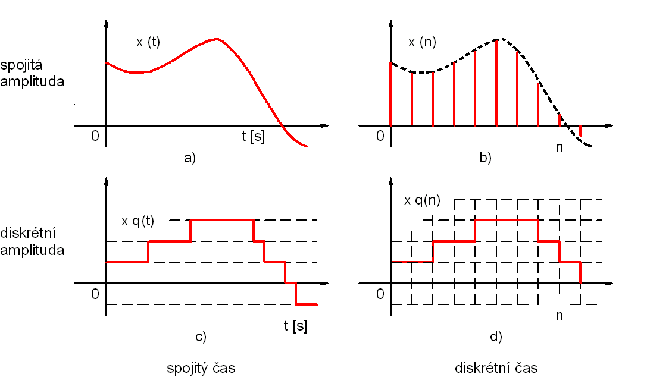
Obr. 1 - Rozdělení signálů z hlediska spojitosti v obou osách
Z hlediska spojitosti v čase a v amplitudě popisuje signály obr. 1. Signály v obr. 1 a jsou tzv. analogové signály, které se vyskytují v analogových obvodech a jsou spojitými funkcemi argumentu t definovanými pro libovolné t. V praxi jde o reálné funkce, jejichž argumentem je čas.
Signály z obr. 1 b jsou signály diskrétní v čase. Mohou nabývat libovolné hodnoty amplitudy v určitém pásmu. Jejich teorie je zpracována ve většině prací týkajících se "číslicového zpracování signálů". Signály tohoto typu zpracovávají obvody s nábojovou vazbou (CCD - charge-couple devices) a filtry se spínanými kapacitory (SCF - switched-capacitor filters).
Signály z obr. 1 c jsou víceúrovňové signály spojité v čase. V praxi se vyskytují většinou pouze jako dvouúrovňové nebo trojúrovňové.
Signály z obr. 1 d jsou vzorkované číslicové signály. V praxi se většinou získávají digitalizací )tj. vzorkováním, kvantováním v úrovni a kódováním) analogových signálů. S tímto druhem signálů pracují všechny číslicové počítače, včetně signálových procesorů. Počet amplitudových úrovní signálu je určen počtem bitů použitého analogově - číslicového převodníku., případně délkou registrů použitého počítače. V teorii se kvantování signálu zohlední zavedením generátorů kvantovacího šumu do blokových schémat popisujících systémy pracující se signály z obr. 1 b, a to v místech, kde ke kvantování dochází.
Signály diskrétní v čase (z obr. 1 b,d) jsou z matematického hlediska posloupnosti. Přechod od analogových signálů k těmto posloupnostem se provádí operací zvanou vzorkování, při kterém je nutno dodržet vzorkovací větu.
Základní pojmy teorie signálu:
Signál je časově proměnná veličina, jíž jsou zobrazovány údaje. Je to jedna z možných fyzikálních vyjádření zprávy.
Analogový signál (spojitý) je signál, který nabývá nespočetného počtu hodnot.
Číslicový signál (diskrétní) je signál, který nabývá spočetného počtu hodnot, tj. jeho hodnoty lze očíslovat, vyjádřit celými čísly a lze je zakódovat do posloupnosti celých čísel
Podle povahy definičního oboru signály dělíme takto:
Signál se spojitým časem je signál, jehož definičním oborem je časový interval
Posloupnost je signál, jehož definičním oborem je spočetná množina hodnot času. Nejčastěji jsou to hodnoty času, ve kterých je signál určen vzorkováním
Impulzní signál = posloupnost
Determinovaný signál je popsaný (tj. průběh dokážeme s dostatečnou přesností aproximovat) nenáhodnou funkcí času: hodnotu signálu můžeme určit pro libovolný čas
Náhodný signál (stochastický)je signál, který lze popsat náhodnou funkcí času:, tj. statistické charakteristiky signálu dokážeme s požadovanou přesností aproximovat charakteristikami náhodné funkce času: v libovolném čaase potom můžeme určit jeho statistické charakteristiky, avšak nikoli jeho hodnotu.
Kauzální signál je determinovaný signál, který má před svým počátkem v čase ta nulovou hodnotu
Finitní signál je signál s nenulovou hodnotou na konečném časovém intervalu. Fyzikálně mohou existovat, oprostíme - li se od kosmologických úvah, pouze finitivní signály.
Kmitání a vlna
Kmitání popisuje časově periodickou závislost amplitudy. Jako příklad uvedu sinusové kmitání (obr. 2)
|
a = Am sinα |
(1) |
kde α je úhel natočení,
Am maximální dosažitelná hodnota, tj. vrcholová amplituda,
a okamžitá hodnota závislá na úhlu natočení α
ω úhlová frekvence
2π oblouková míra natočení o 360°
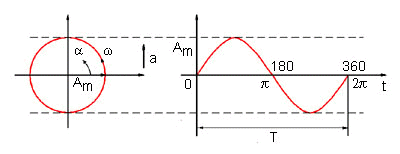
obr. 2 - Sinusový kmit
Elektricky můžeme na amplitudu nahlížet jako na napětí, proud, výkon atd. Často bývá jako amplituda udávána efektivní hodnota
|
Aef = Am / √2 |
(2) |
Jako amplituda bývá uváděna i amplituda mezi dvěma vrcholky
|
Avv = 2Am |
(3) |
Pro závislost úhlu natočení α° na obloukové míře ά nebo na času t (s) lze udat vztahy
|
α° / 360° = α / 2π = t / T = tf |
(4) |
kde 2π je oblouková míra natočení o 360°, T je doba trvání jednoho kmitu, nazývaná také perioda.
Obrácená hodnota 1/T = f je frekvence v 1/s = Hz (hertz). Udává počet kmitů za sekundu.
Po úpravě vztahu, kdy ά = 2π ft = ωt, kde ω je úhlová frekvence, dostaneme
|
a = Am sin ωt |
(5) |
Nezačíná-li kmit na nule, je nutné brát v úvahu fázový posun φ, např. při posunutí doprava o úhel φ je
|
a = Am (sin ωt - φ) |
(6) |
2.1 Tvary signálů
Testovací signály jsou to signály, které dokážeme analyticky popsat a opakovaně vygenerovat.
Patří mezi ně:
2.1.1 Heavisideův skok H(x), z nějž získáme přechodovou charakteristiku.
|
Pro Heavysideův skok platí:
H(x) = 0, pro x<0 ; H(x) = 1, pro x≥0
|
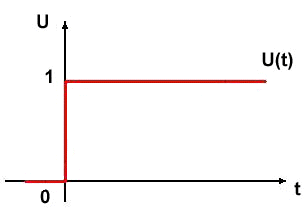 obr. 3 - Heavysideův skok |
2.1.2 Diracův impuls
V teorii spojitých signálů a systémů má důležitou roli speciální signál, nazývaný Diracův impuls, δ - impuls, případně δ - funkce. Jde o signál v praxi realizovatelný pouze přibližně. Jeho délka je nekonečně malá a amplituda nekonečně velká, přičemž jeho plocha je rovná jedné (proto se nazývá jednotkový impuls). Z matematického hlediska jde o zobecněnou funkci neboli distribuci. Výklad teorie distribuce nebudu zmiňovat, uvedu jen základní informace, které umožní zjednodušit některá dále uvedená odvození. Zejména využijeme toho, že násobení signálu posloupností Diracových impulsů je ekvivalentní vzorkování signálu v okamžicích těchto impulsů.
Diracův impuls lze definovat jako limitu posloupnosti určitých funkcí f (t) pro délku těchto funkcí blížící se nule. Nejjednodušší funkcí použitelnou v roli vytvářející funkce je pravoúhlý impuls dle obrázku 4 a). Pokud jde šířka tohoto impulsu k nule a přitom se zachovává jednotková plocha impulsu, stává se impuls nekonečně krátkým a nekonečně vysokým. Platí pro něj tedy
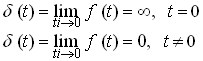 |
(7) |
a současně
|
|
(8) |
Pro δ - impuls posunutý o hodnotu t platí
|
|
(9) |
a současně
|
|
(10) |
Z výše uvedených vztahů plyne vzorkovací vlastnost δ - impulsu:
|
|
(11) |
kde jsme použili vztah (). Protože δ (t) je sudá funkce, platí také:
|
|
(12) |
Chceme - li vypočítat spektrum funkce δ(t), dosadíme do definičního vztahu pro přímou Fourierovu transformaci:
|
|
(13) |
za funkci x (t) obdélníkovou vytvořující funkci dle obrázku 4 a). Výpočtem integrálu a limity (výpočet l'Hospitalovým pravidlem) dostaneme:
|
|
(14) |
Diracův impuls budeme značit šipkou dle obrázku 4 b). Pokud bude váha (plocha) impulsu odlišná od 1, bude její hodnota vyjádřena číslem u šipky nebo naznačena délkou šipky. Použijeme -li pro vyjádření souvislosti mezi předmětem a obrazem Fourierovy transformace symbol ↔, můžeme psát:
|
δ (t) ↔ 1 |
(15) |
Odtud plyne, že spektrum Diracova impulsu je reálné a má tedy nulovou fázi.
Další důležité vlastnosti Diracova impulsu jsou:
|
x (t)δ (t - t0) = x (t)δ (t-t0), |
(16)
|
|
x (t)*δ (t - t0) = x (t-t0), |
(17)
|
|
aδ (t) ↔ a, |
(18)
|
|
δ (t - t0) ↔ e-jωt0, |
(19)
|
|
δ (at) = (1 / |a|)* δ (t), |
(20)
|
Důležitá je zejména skutečnost, že konvolucí libovolné funkce s Diracovým impulsem posunutým do bodu t je tato funkce posunutá o stejnou hodnotu. Pro nulový posuv odtud vyplývá, že konvolucí určité funkce s Diracovým impulsem je nezměněná původní funkce:
|
x (t)*δ(t) = x (t) |
(21) |
Význam Diracova impulsu spočívá mimo jiné v tom, že odezvou lineárního spojitého systému je tzv. impulsní odezva (váhová funkce) h (t) a konvolucí impulsní odezvy systému a vstupního signálu je výstupní signál systému.
|
obr: 4 - Obdélníková vytvořující funkce
|
obr. 5 - Diracův impuls |
2.1.3 Rampový průběh _/¯(x), jehož vlivem získáme odezvu systému, jehož úpravou získáme přechodovou charakteristiku.
|
Kde platí:
0 ; x < ‑1/2 _/¯(x) = { x + 1/2 ; |x| < 1/2 1 ; x > 1/2
|
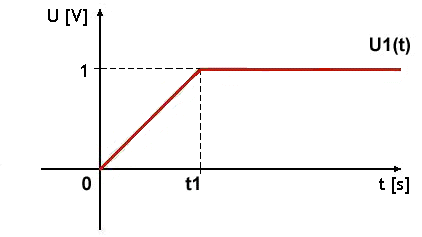 obr. 6 - Rampový průběh |
2.1.4 Trojúhelníkový impuls
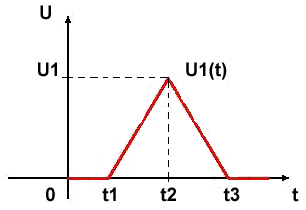 obr. 7 - Trojúhelníkový impuls |
2.1.5 Pilovitý impuls
|
obr. 8 - Pilovitý impuls |
2.1.6 Lichoběžníkový impuls
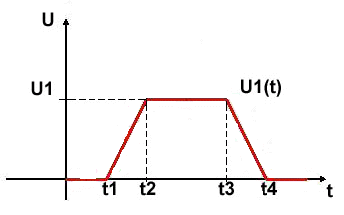 obr. 9 - Lichoběžníkový impuls |
2.1.7 Pravoúhlý (obdélníkový) puls
|
obr. 10 - Pravoúhlý puls
|
2.1.9 Harmonický signál, z jehož odezvy systému získáme po úpravě frekvenční charakteristiku, popis a vzhled signálu viz výše.
2.1.10 Vysokofrekvenční signál
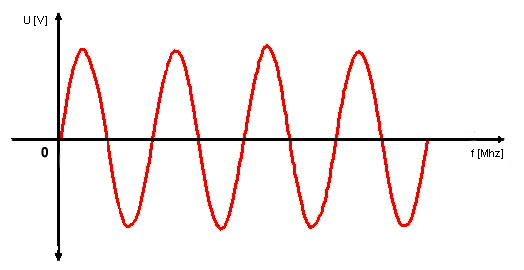 obr. 11 - Vysokofrekvenční signál |
2.1.11 Nízkofrekvenční signál
|
obr. 12 - Nízkofrekvenční signál
|
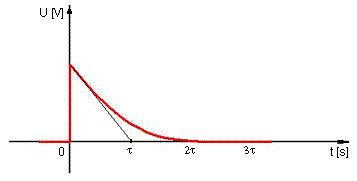
obr. 13 - Exponenciální impuls
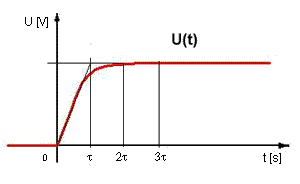
obr. 14 - Exponenciální čelo impulsu