3.6 Zapojení s pasivními součástkami:
Kmitočtově závislé obvody:
Přísně vzato nelze žádný prvek považovat za dokonale lineární a kmitočtově nezávislý pro teoreticky nekonečný rozsah napětí a kmitočtu. Nadále však budeme považovat za kmitočtově závislé obvody pouze zapojení, ve kterých se vyskytuje reaktance. Tyto obvody s kondenzátory a cívkami mají v elektronice velmi široké použití, např. jako filtry.
Fázorový počet v elektronice
Pro matematický popis těchto obvodů se s výhodou používá komplexní počet. Základní rozdíl proti předchozím výpočtům spočívá ve vektorovém charakteru veličin. Napětí, proud, ale i zdánlivý odpor – impedance mají nejen velikost, ale i směr (počáteční fázový posuv), takže je nelze jednoduše sčítat.

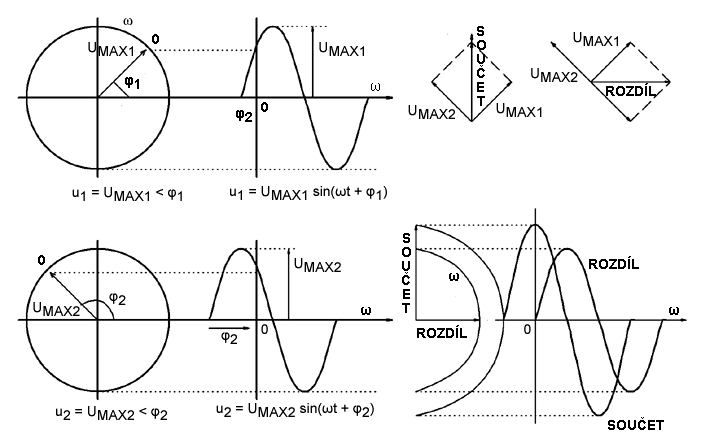
obr. 36 - Vektorový součet a rozdíl dvou harmonických napětí
Na obrázku je znázorněna známá grafická metoda odvození sinusového (harmonického) průběhu signálu
| u = U sin(ωt + φ) |
(45) |
pomocí průvodiče rotujícího konstantní úhlovou rychlostí ω = α/t. (v elektrotechnice je úhlová rychlost nazýván úhlový kmitočet a má stejnou jednotku rad/s)
Celou kružnici (otočení o úhel 2π) vektor opíše za dobu periody T, takže musí platit
| ω = 2π /T , |
(46) |
nebo po dosazení za kmitočet
| (f = 1/T) ω = 2πf |
(47) |
Představa rotujícího vektoru umožňuje snadné sčítání nebo odčítání harmonických signálů se stejným kmitočtem a s rozdílnými počátečními fázovými posuvy φ. Vektory samozřejmě není nutné sčítat graficky, ale je možné je rozložit na pravoúhlé složky a sčítat nebo odečítat podle pravidel pro počítání s vektory. Protože je zažité počítání s efektivními hodnotami harmonického průběhu
| U = UMAX/ √2 , |
(48) |
kreslí se i fázorové diagramy pro efektivní hodnoty.
I když je možné vystačit pro praktické výpočty s představou rotujících časových vektorů (fázorů), dává se při praktických výpočtech přednost tzv. symbolickému počtu v komplexní rovině. Oproti matematice se pro imaginární svislou složku vektoru nepoužívá písmenko i, protože by se pletlo s okamžitou hodnotou proudu, ale písmenko j = √-1. Každý bod v komplexní rovině má reálnou (vodorovnou) a imaginární (svislou) souřadnici. Komplexní veličina bude pro rozlišení značena tučným písmem, např. Z = R +jX. Kromě složkového tvaru lze komplexní číslo zapsat v trigonometrickém tvaru: Z = |Z| .(cos φ + j.sinφ). Závorku také lze nahradit praktičtějším exponenciálním tvarem Z = |Z|ejω .Tento tvar odpovídá vyjádření vektoru velikost/úhel:Z = Z < φ a používá se při násobení a dělení komplexních čísel. Složkový tvar je naopak výhodnější pro operace sčítání a odečítání. Vzájemné převody bývají k dispozici na kalkulátorech.
Podobně jako se ve fyzice rozlišuje průměrná rychlost a okamžitá rychlost, je možné definovat průměrný proud
| I = Q / t |
(49) |
a okamžitý proud jako změnu náboje
| i = dQ/dt. |
(50) |
Pro náboj na kondenzátoru platí:
| Q = C.u. |
(51) |
Po dosazení získáme vztah:
| i = C du/dt, |
(52) |
nebo po úpravě
| u = 1/C ∫ idt. |
(53) |
To, že proud kondenzátorem je derivací napětí na kondenzátoru, můžeme využít pro odvození impedance kondenzátoru. Bude – li podle předchozího obrázku mít vstupní napětí sinusový průběh (u = UMAX sin 2πft), získáme po derivaci:
| i = C.UMAX 2πfcos 2πft. |
(54) |
Protože člen před kosinovou funkcí má význam amplitudy proudu, vyplývá z toho, že:
| UMAX / IMAX = U. √2 / I . √2 = 1/ 2πfC = XC. |
(55) |
Má rozměr ohmu. Veličina se nazývá kapacitní reaktance a je nepřímo úměrná kmitočtu. Protože funkce kosinus předbíhá funkci sinus o devadesát stupňů, říkáme, že u kondenzátoru proud předbíhá napětí. Fázory jsou posunuty o 90° takže:
| Z = U < 0 / I < π/2 = Z < - π/2 |
(56) |
Výsledná impedance má tedy fázový posuv – 90°, a je proto záporně imaginární Z = -jXC. U operátorového počtu bývá zvykem sdružovat imaginární člen s kmitočtem, takže po úpravě rozšířením (j2 = -1) je:
|
|
(57) |
Stejným způsobem lze z indukčního zákona
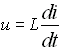 |
(58) |
odvodit indukční reaktanci cívky Z = jωL, která je přímo úměrná kmitočtu. Napětí na cívce předbíhá proud o 90°. Obě reaktance jsou čistě imaginární a z důvodu posuvu mezi napětím a proudem je vždy po čtvrtinu periody součin napětí a proudu kladný a po čtvrtinu záporný. To znamená, že elektrostatické nebo elektromagnetické pole vzniká a odebírá energii ze zdroje a pak zaniká a dodává energii zpět do zdroje. Na rozdíl od rezistoru, který má napětí i proud ve fázi, nevzniká tedy v ideálním kondenzátoru nebo cívce žádné teplo, pouze dochází k cyklické výměně energie mezi reaktancí a zdrojem. Tohoto poznatku se někdy používá k návrhu bezztrátových předřadníků.
Komplexní jednobrany
Protože s rostoucím počtem prvků roste složitost matematického popisu obvodu, omezíme se pouze na nejjednodušší RLC obvody. Vektorové čáry u těchto základních obvodů jsou podle typu rovnice pro impedanci buď (polo)přímky (), anebo (polo)kružnice (()) procházející počátkem.Kmitočet je pouze kladný. Pro sériové spojení odporu a cívky jsme odvodili:
| Z = R + jωL |
(59) |
a podobně pro sériové spojení odporu s kondenzátorem bude:
| Z = R – j (ωC)-1 . |
(60) |
Těmto rovnicím odpovídají polopřímky kolmé na reálnou osuv bodě R. Pro paralelní zapojení RL lze z trojúhelníku vodivosti odvodit:
| Y = G – jXL-1. |
(61) |
Protože impedance je převrácenou hodnotou admitance, bude vektorovou čarou polokružnice stejně jako u paraleního zapojení RC:
| Y = G + jXC-1. |
(62) |
Pro sériové spojení RLC, tzv. rezonanční obvod, lze stejným způsobem odvodit impedanci:
| Z = R + j (XL – XC ). |
(63) |
Řešením je v tomto případě celá přímka, protože když ωL roste, (ωC)-1 klesá a opačně. Pro paralení rezonanční obvod je:
| Y = G – j( XC-1 – XL-1). |
(64) |
Impedanční charakteristika tvoří kružnici o průměru 1/G. Charakteristiky RLC obvodů lze získat složením obou částí obrázku.
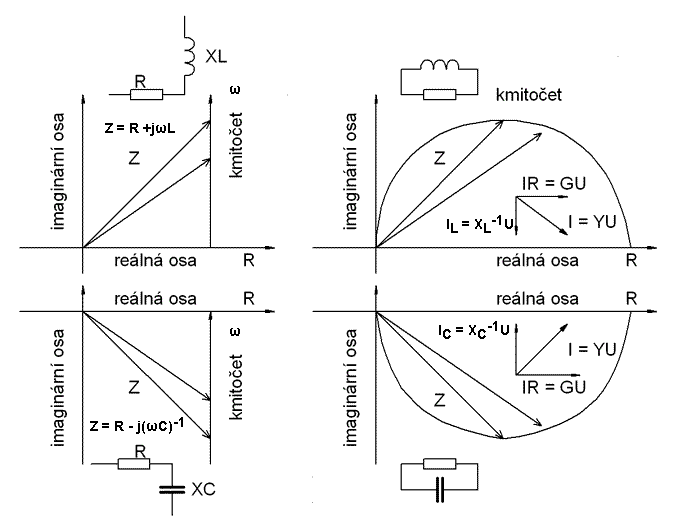
obr. 37 - Komplexní charakteristiky jednoduchých RC a RL obvodů
Porovnáním vektorových čar, nazývaných též komplexní kmitočtové charakteristiky, lze dospět k závěru, že pomocí RLC obvodů lze při vhodné volbě prvků a kmitočtu dosáhnout libovolnou hodnotu impedance. Protože obvod nebývá záporný, je oblast omezena pouze na kladnou komplexní polorovinu. Jednoduššími obvody lze pokrýt pouze jeden kvadrant. Pokud je ale kmitočet pevně dán, je možné stejného bodu roviny dosáhnout paralelním i sériovým spojením prvků. Takovéto obvody, které mají stejnou impedanci při daném kmitočtu, ale liší se zapojením, se nazývají duální obvody. Grafické znázornění řešení představuje průsečík polopřímky s polokružnicí za podmínky, že k průniku dojde při stejném kmitočtu.
Pro napětí na sériovém spojení RC prvků platí podle II. Kirchhoffova zákona rovnice:
| u1 = R . i + uC = R . CduC / dt + uC . |
(65) |
Bude-li konstanta RC hodně velká vzhledem k periodě uvažovaného signálu, bude možné zanedbat druhý člen rovnice
| (u ≈ RCduC / dt). |
(66) |
Výstupní napětí kmitočtově závislého děliče pak bude přibližně integrálem vstupního napětí:
| uC = u2 = 1/RC ∫ u1dt. |
(67) |
V případě harmonického vstupního napětí se nebude měnit tvar signálu, pouze k posuvu téměř o 90°:
| ∫ sinxdx = - cosx = sin (x - π/2). |
(68) |
Budou - li na vstupu článku obdélníky, získáme přibližně trojúhelníkový výstupní signál, protože:
| ∫ kdx = kx |
(69) |
a
| ∫ -kdx = -kx. |
(70) |
Rovnice y = kx je rovnice přímky. Podobné vztahy lze odvodit i pro sériové spojení RL.
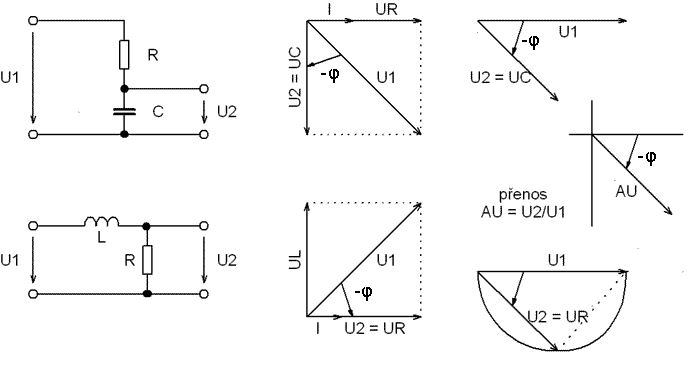
obr. 38 - Podobnost fázorových diagramů integračních článků
Až na počáteční posuv jsou diagramy shodné, takže vlastnosti obou článků jsou stejné. Oba tvoří kmitočtově závislý dělič, jehož přenos se s rostoucím kmitočtem zmenšuje. V prvním případě se s rostoucím kmitočtem zmenšuje reaktance kondenzátoru, a výstupní napětí UC = XCI se proto blíží nule. V druhém obvodu rostoucí reaktance cívky zvětšuje celkovou impedanci, a proud obvodem se proto s kmitočtem zmenšuje. Výstupní napětí UR = RI bude tedy opět malé. S rostoucím kmitočtem se bude výstupní napětí zmenšovat a fázový posuv se bude blížit devadesáti stupňům. Obvod začne integrovat. Protože U1 je konstantní a zbývající napětí jsou na sebe kolmá, bude vektorovou čarou Thaletova kružnice.
Obvody s přesně opačnými vlastnostmi lze získat velmi jednoduše pouhým prohozením prvků. Pro sériové spojení RC s odporem na výstupu lze analogicky odvodit:
| u1 = uC + uR = 1/C ∫ idt +uR. |
(71) |
Po dosazení za proud i = u /R a zanedbáním členu u dostaneme:
| u1 ≈ 1/RC ∫ uRdt. |
(72) |
Odintegrováním rovnice dostaneme výsledný přibližný vztah:
| uR = u2 = RC du1/ dt |
(73) |
V případě harmonického signálu se opět tvar signálu po průchodu článkem nemění. Fázový posuv o π/2 bude opačným směrem ((sinx)' = cosx). Podobně ze vstupního trojúhelníkového signálu získáme obdélníky((kx)' = k). Obvod bude dobře derivovat v případě, že se fázový posuv bude blížit devadesáti stupňům. Tzn., že perioda vstupního signálu nyní musí být mnohem větší, než je konstanta RC. Pro obvod RL lze opět odvodit podobné rovnice.
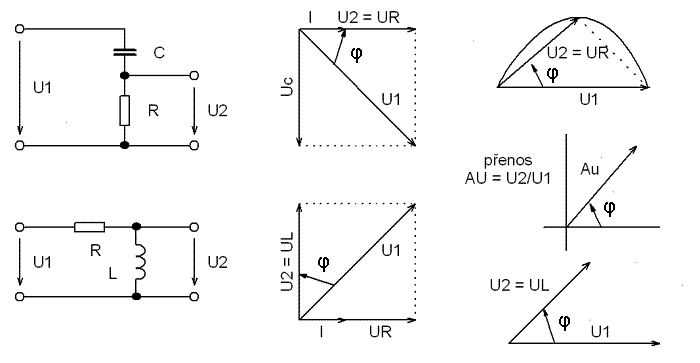
obr. 39 - Fázorové diagramy derivačních článků
Od integračních článků se derivační obvody liší pouze umístěním výstupu, takže fázorové diagramy pro napětí a proud musí být shodné. Tyto kmitočtově závislé děliče mají přesně opačné vlastnosti. U RC obvodu se s rostoucím kmitočtem zmenšuje reaktance kondenzátoru a proud obvodem vzrůstá. Větší proud vyvolá na odporu větší výstupní napětí
| UR = RI. |
(74) |
U druhého zapojení si lze představit, že rostoucí reaktance cívky mění dělicí poměr děliče ve prospěch výstupního napětí:
| UL = XLI. |
(75) |
Paralelním spojením prvků lze analogicky získat proudové kmitočtově závislé děliče, které budou mít opět integrační a derivační charakter pro vstupní proud.
Wienův článek
Tato pásmová propust se často používá ve zpětné vazbě RC generátorů. Má nejmenší selektivitu (nejširší pásmo) a nejmenší přenos ze zatím probraných obvodů. Oproti těmto obvodům se ale vyznačuje velmi jednoduchou přeladitelností současnou změnou dvou stejných prvků. Protože druhá impedance je tvořená paralelním spojením dvou prvků, je pro odvození přenosu nejvýhodnější rovnice:
| A = 1/ (ZY + 1). |
(76) |
Po dosazení za impedanci
| Z = R + 1/jC |
(77) |
a admitanci
| Y = 1/R + jC |
(78) |
dostaneme po roznásobení vztah:
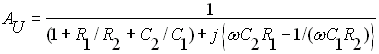 |
(79) |
Přenos bude čistě reálný při tzv. kvazirezonančním kmitočtu:
|
(80) |
Většinou se volí prvky tak, aby platilo: R1 = R = nR2 a C1 = C = C2 /n. Po dosazení se vztahy zjednodušší:
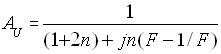 |
(81) |
a
| ω0 = 1/RC, (F = ω/ω0). |
(82) |
Volbou n je možné měnit velikost přenosu při kvazitolerančním kmitočtu. Bohužel se n objevilo i u imaginárního členu, a proto není vhodné volit n < 1. Přenos by se sice zvětšil:
| AUMAX = 1/ (1 + 2n), |
(83) |
ale téměř by se neměnil s kmitočtem. Řešením rovnice pro rovnost imaginárního a reálného členu ve jmenovateli opět získáme:
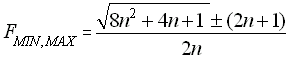 |
(84) |
a šířku pásma propusti:
| BREL = 2 + 1/n |
(85) |
Porovnáme-li vztah pro maximální přenos a pro šířku pásma, zjistíme, že optimální článek má prvky stejné (n = 1). Pak bude platit:
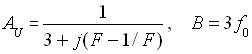 |
(86) |
a
|
(87) |
|
obr. 40 - Charakteristiky Wienova článku |