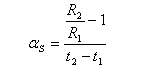Zadání:

1. Vypočtěte hodnotu součinitele as platinového odporového teploměru Pt-100 v rozmezí asi 20°C – 95°C .
2. Vypočtěte výslednou náhodnou chybu das (absolutní a relativní), a určete, která z měřených veličin nejvíce ovlivní výslednou chybu

Teoretický úvod:

a) Měření teploty odporovými teploměry je založeno na změně elektrického odporu vodiče při změně jeho teploty. Každé změně teploty v malém rozmezí odpovídá změna odporu, kterou odvodíme ze známého vztahu mezi odporem kovu a teplotou:

R₂ = R₁ (1+a_S (t₂ – t₁)) ....(1)

kde

R₁, R₂ – hodnoty odporů při teplotách t₁, t₂

t₁, t₂ – měřené teploty

a_S – součinitel odporu v rozmezí teplot t₁ - t₂

Z uvedené rovnice pak :

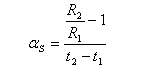(2)

Pro maximálně přesné zjištění součinitele odporu ls je nutno vycházet z přesného měření jednotlivých odporů platinového odporového teploměru.

b)  Při měření teploty rtuťovým teploměrem se většinou měří při úplně ponořeném teploměru, pokud na teploměru není stanoveno jinak. Pokud není proveden úplný ponor teploměru, je nutno provést přepočet na ochlazení vyčnívajícího rtuťového plátna a kapiláry. Při korekci se bere v úvahu rozdíl měřené teploty a teploty okolí teploměru (t₂ – t₀), délka vyčnívajícího vlákna rtuti vyjádřená počtem “vyčnívajících“ stupňů (n) a druh skla, který určuje součinitel roztažnosti rtuti ve skle ao.

Korekce se vypočte :

(3)

A správná hodnota teploty :

(4)

Součinitel lo se pro běžné případy volí ao = 1/6300. Pro speciální druhy skla, mající zvláštní zabarvení nebo vtavený barevný pásek, jsou tyto součinitele předepsány. Při měření se okolní teplota zjišťuje asi uprostřed vyčnívajícího rtuťového vlákna.

c) Počítáme-li hodnotu součinitele odporu, který je funkcí více naměřených veličin (t₁, t₂, R₁, R₂), bude výsledná hodnota dána vztahem (2).

Jestliže je každá naměřená veličina (t₁, t₂, R₁, R₂) zatížena náhodnou chybou , pak výsledná náhodná chyba absolutní

je dána vztahem 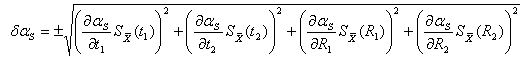(5):

(5)

Kde náhodné chyby arytmických průměrů jsou dány vztahem 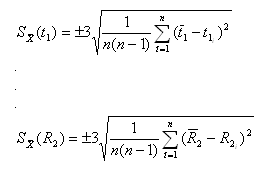/6/ :

(6)

Při měření teploty rtuťovým teploměrem musíme uvažovat mimo náhodné chyby měření ( ± S_X(t₁),…) ještě systematickou chybu teploměru, která je dána jeho rozlišovací schopností SR(t1) (polovina nejmenšího dílku na stupnici teploměru). Proto výsledná chyba měření teploty, jež bude dosazena do (5), bude mít tvar:

(7)

a vztah pro výpočet výsledné náhodné chyby absolutní :

(8)

Výsledná chyba relativní je dána vztahem:

(9)

Popis zařízení:

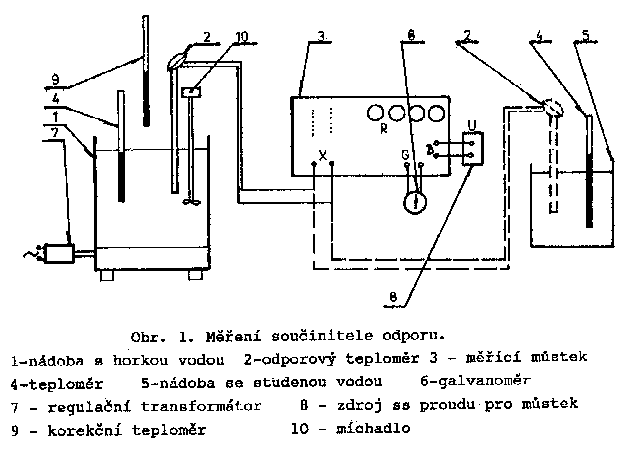
Ve vytápěné nádobě (1) je umístěn platinový odporový teploměr (2) a rtuťový kontrolní teploměr (4) a teploměr korekční (9).Odpor platinového teploměru je měřen Wheatstoneovým můstkem (3). Po změření hodnoty odporu v horké vodě je možno teploměr (1) přemístit do nádoby (5) se studenou vodou, kde je teplota kontrolována rtuťovým teploměrem (4).

Postup práce:

1. Měřený teploměr je v chladné vodě. U nádoby s ohřívanou vodou zapnout topení, a udržovat teplotu vody co nejstabilnější. Tuto teplotu zvolte v rozmezí 70 – 95°C . Mezitím měřit 10x odpor teploměru v chladné vodě, odečty měřícího můstku provádět co nejpřesněji, případně interpolovat mezi nejnižšími nastavitelnými hodnotami podle výchylek paprsku galvanoměru. Po každém odečtu mírně rozvážit dekádu můstku. Po této sérii měření přemístit odporový teploměr do horké vody, nechat ustálit a opět měřit 10x. Na rtuťových teploměrech odečíst teplotu měřených prostředí. Pro přesnější odečet je možno vždy jemně na teploměr poklepat. Zároveň je nutno brát v úvahu teplotu okolíé a vyčnívající sloupec rtuti (výpočet korekce na vyčnívající sloupec rtuti dle vztahu 3).
2. Z jednotlivých měření se vypočte aritmetický průměr a jeho chyba, u skleněných teploměrů se uvede rozlišovací schopnost. Při měření odporu teploměru je nutno odečíst odpor vedení. (Rv = 0,09 W ). U skleněných teploměrů se bere pro další výpočet chyba výsledná dána vztahem (7).
3. Změřené a vypočtené výsledky se dosadí do vzorce pro součinitel odporu a vypočte se jeho výsledná náhodná chyba absolutní (8) a relativní (9). Do vzorců (2),(3),(4),(8) dosazujeme aritmetické průměry veličin

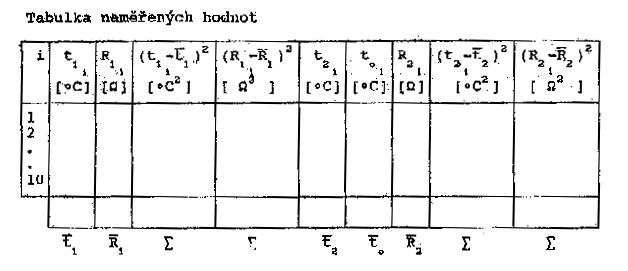
Tabulka naměřených hodnot:

Kontrolní otázky:

1. Zpracování náhodných chyb
2. Co je střední teplotní součinitel odporu?
3. Jak se správně měří rtuťovým teploměrem, vztah pro korekci.
4. Uveďte vztah závislosti odporu kovu na teplotě.

Pracoviště 4:      Součinitel odporu      Termistory