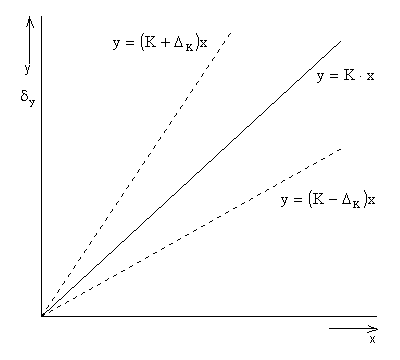V případě
vyjádření číslicového slova 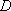 v přirozeném binárním kódu odpovídá analogové váze nejméně významného
bitu (LSB - Least Significant Bit) šíře pásma
v přirozeném binárním kódu odpovídá analogové váze nejméně významného
bitu (LSB - Least Significant Bit) šíře pásma 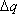 .
Z tohoto důvodu se chyby
senzoru s číslicovým výstupem, podobně jako chyby analogově-číslicového
převodníku, vyjadřují v celých násobcích 1/2 LSB. .
Z tohoto důvodu se chyby
senzoru s číslicovým výstupem, podobně jako chyby analogově-číslicového
převodníku, vyjadřují v celých násobcích 1/2 LSB. |
Pro relativní
chybu senzoru s číslicovými výstupem platí |
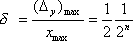 |
(1.10) |
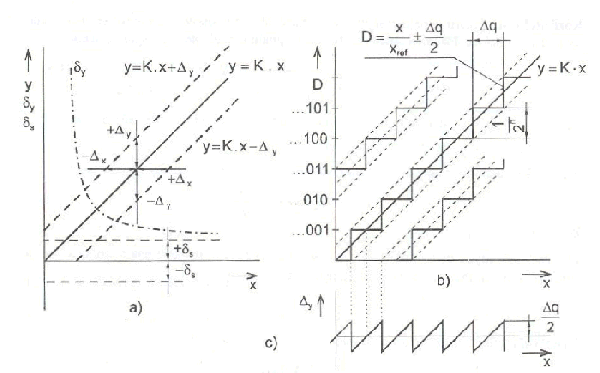
Multiplikativní
chyba senzoru je ekvivalentní změně citlivosti senzoru. Statická charakteristika
má odlišný sklon od jmenovité charakteristiky. |
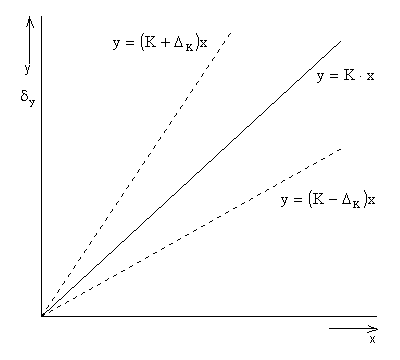
Multiplikativní chyba
|
Hodnota absolutní m
ultiplikativní chyby 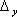 je tedy závislá na hodnotě měřené veličiny. Platí vztahy
je tedy závislá na hodnotě měřené veličiny. Platí vztahy |
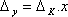
|
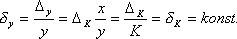 |
(1.11) |
nebo-li chyba měření
je konstantní ( 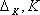 jsou konstanty). Multiplikativní chyba je způsobena např.
změnou odporové sítě zesilovačů, vlivem parazitních veličin (např. teploty),
aj. Výrobci senzorů multiplikativní chybu označují jako relativní chybu
z měřené hodnoty. Je-li známa multiplikativní a aditivní chyba senzoru,
je výsledná chyba měření dána
jsou konstanty). Multiplikativní chyba je způsobena např.
změnou odporové sítě zesilovačů, vlivem parazitních veličin (např. teploty),
aj. Výrobci senzorů multiplikativní chybu označují jako relativní chybu
z měřené hodnoty. Je-li známa multiplikativní a aditivní chyba senzoru,
je výsledná chyba měření dána |
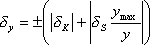 resp.
resp. 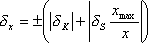
|
(1.12) |
Na základě
znalosti aditivních chyb 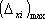 , ,
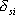 a multiplikativních chyb
a multiplikativních chyb 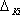 , ,
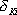 jednotlivých bloků
měřicího řetězce lze vypočítat výslednou chybu řetězce. Pro sériově
řazený řetězec s
jednotlivých bloků
měřicího řetězce lze vypočítat výslednou chybu řetězce. Pro sériově
řazený řetězec s  bloky platí
bloky platí |
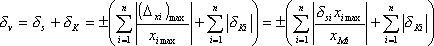 |
(1.13) |
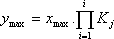
|
Pro paralelně
řazený řetězec s bezchybovým sumačním členem platí
|
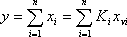 |
(1.14) |
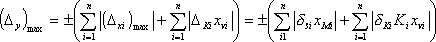 |
(1.15) |
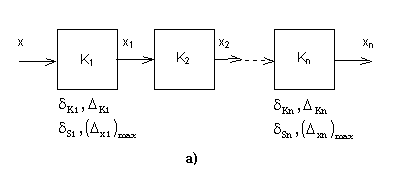 |
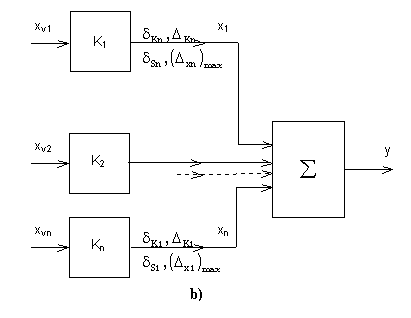
Měřicí řetězec (a - sériový, b - paralelní)
|
Podobné
vztahy lze odvodit pro zpětnovazební řetězec aj. Uvedené vztahy reprezentují
největší množství chyb. Ve skutečnosti se při více členech měřicího řetězce
uplatňují obě polarity chyb, a proto výsledná chyba je obvykle menší.
Z tohoto důvodu se často používá vztah platný pro výslednou směrodatnou
odchylku více nezávislých náhodných chyb. Výsledná chyba se označuje
jako efektivní a počítá se dle vztahu
|
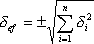 |
(1.16) |
Uvedený
vztah by byl platný pro výslednou směrodatnou odchylku jen tehdy, pokud
by výrobci uváděli chyby také jako směrodatné odchylky nebo krajní chyby
(trojnásobek směrodatné odchylky).
|
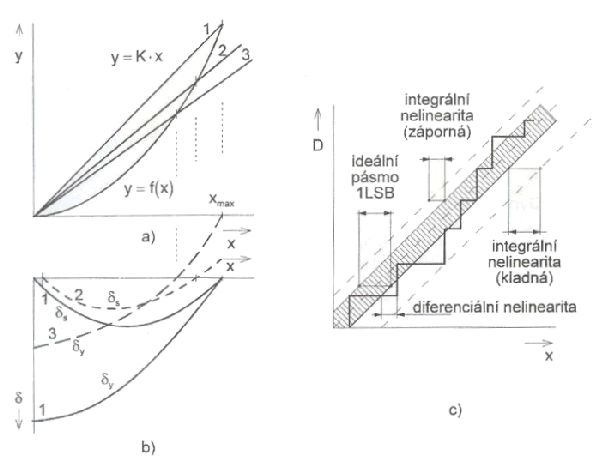
Chyba linearity
senzoru je dána odchylkou od lineární (spojité analogové nebo kvantové)
charakteristiky. Pro analogový signál se chyba linearity udává vztahem
|
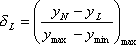 |
(1.17) |