Chyby a nejistoty měření
Chyby měření      Nejistoty měření
Chyby měření

       V praxi nejsou žádné měření, žádná měřicí metoda ani žádný přístroj absolutně přesné. Nejrůznější negativní vlivy, které se v reálném měřicím procesu vyskytují, se projeví odchylkou mezi naměřenou a skutečnou hodnotou sledované veličiny. Výsledek měření se tak vždy pohybuje v jistém „tolerančním poli“ kolem skutečné hodnoty, ale téměř nikdy nenastává ideální ztotožnění obou hodnot.

       Za dlouhá léta používání bylo zvykem při vyhodnocování souborů naměřených hodnot pracovat s chybami.

       Chyby se vyjadřují v absolutních nebo relativních odchylkách. Podle jejich působení lze chyby rozdělit na systematické, náhodné a hrubé. Podle svého zdroje se rozdělují na chyby přístroje, metody, pozorování a vyhodnocení. Jako chyba absolutní  se označuje rozdíl mezi hodnotou naměřenou   a skutečnou  . Rozdělí-li se absolutní chyba na skutečnou hodnotu, dostane se poměrné vyjádření chyby, tj. relativní chyba .

       Systematické chyby jsou při stálých podmínkách také stálé co do velikosti tak i znaménka a svým působením systematicky ovlivňují výsledek měření. Ke stanovení jejich velikosti zpravidla postačí vztah

(1.38)

       Z hlediska uživatele měřicí techniky jsou systematické chyby sympatické tím, že je lze z velké části určit a jejich vliv je možné zmenšit například pomocí korekcí, kompenzací apod. Takto se zpravidla podaří odstranit podstatnou část jejího negativního vlivu na měření, ale zůstane ještě zbytek, který lze označit jako nevyloučené (nevyloučitelné) systematické chyby.

       Náhodné chyby působí zcela nahodile, jsou těžko předvídatelné a nelze je vyloučit. Při opakování měření se mění jejich velikost i znaménko, jak odpovídá předpokládanému zákonu rozdělení. Pro určení jejich velikosti se vychází z opakovaných měření s použitím statických metod odpovídajících patřičnému pravděpodobnostnímu modelu, reprezentovanému zákonem rozdělení příslušné náhodná chyby. V praxi velmi často jde o rozdělení normální-Gausovo, které se používá ve většině aplikací.

       Výsledek měření, stanovený ze souboru opakovaných měření realizovaných za stejných podmínek, je reprezentován aritmetickým průměrem získaných hodnot při  opakováních z hodnot  tj.

(1.39)

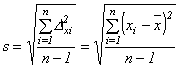       Náhodnou chybu v klasické teorii chyb nejčastěji zastupuje směrodatná odchylka výběrového souboru , méně často směrodatná odchylka aritmetického průměru , získané ze vztahů

(1.40)

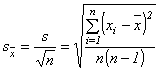(1.41)

       Obě směrodatné odchylky patřičným způsobem blíže charakterizují chování náhodných chyb.

       Hrubé chyby jsou z hlediska předchozího pohledu zcela nevyzpytatelné. Měření zatížené hrubou chybou znehodnotí celý experiment, a proto měřené hodnoty, které výrazně vybočují, což bývá velmi často projevem tohoto druhu chyby, se vyloučí z dalšího zpracování. Výsledná chyba měření je vyjadřována jako součet systematické a náhodné složky, což lze zapsat

(1.42)

       a její maximální hodnotu je možné odhadnout jako

(1.43)

       kde systematická složka , a náhodná složka , popř. . Součinitel rozšíření směrodatné odchylky souvisí s pravděpodobností pokrytí intervalu a typem rozdělení. Dvojka u Gaussova rozdělení přísluší často používané 95% pravděpodobnosti.

       Co se týče původu chyby, chyb přístrojů jsou způsobeny nedokonalostmi použitých měřicích prostředků, které mohou vznikat ve výrobě, montáži a popř. i opotřebením. Svou roli sehrává i změna charakteristik a parametrů přístroje v čase (stárnutí). Dalším zdrojem chyb je nevhodná instalace nebo uložení přístroje na pracovním místě, stole apod. Chyby metody mají svůj původ v nedokonalosti či zjednodušení použité měřicí metody. Chyby pozorování, nebo spíče pozorovatele, jsou do měření vnášeny jako chyby osobní, zapříčiněné buď nedokonalostí smyslů pozorovatele nebo jeho nesoustředěností. Chyby mající svůj původ ve vyhodnocení jsou časté jako výpočtové, vznikající v důsledku aplikování přibližných vztahů, zjednodušení, ale také použitím linearizace, interpolace, extrapolace, zaokrouhlování, nedostatečným vyčíslením konstant apod.

Nejistoty měření
Typy nejistot

       Nejistota je označení pro parametr související s výsledkem měření a charakterizující rozsah hodnot, které je možné racionálně přiřadit k měřené veličině. Nejistota se skládá z několika dílčích nejistot (složek).

       Ke stanovení jejich velikosti jsou principálně k dispozici tyto dvě metody:

-

statistické zpracování naměřených údajů (metoda typu A)

-

jiné než statické zpracování naměřených údajů (metoda typu B)

       Někdy se nejistoty získané metodou A také stručně označují jako nejistoty typu A, obdobně nejistoty získané metodou B jako nejistoty typu B. Z těchto základních typů nejistot se snadno, prostřednictvím součtu jejich čtverců, určí výsledná nejistota kombinovaná.

Nejistoty kombinované a rozšířené

       V praxi se jen zřídka vystačí s jedním nebo druhým typem nejistoty samostatně. Pak je zapotřebí stanovit výsledný efekt kombinovaných nejistot měření obou typů A i B. Výsledná kombinovaná nejistota veličiny  se označuje  a určuje se jako odmocnina ze součtu čtverců obou typů nejistot A a B podle vztahu.

(1.44)

       Tam, kde nestačí standardní nejistoty, je nutné použít k jejich rozšíření . Původně stanovená směrodatná odchylka (tedy i standardní nejistota) představuje např. u nejčastěji používaného normálního rozdělení interval určený s pravděpodobností asi 68%. Podobně je tomu i u jiných zákonů rozdělení. Aby bylo dosaženo lepšího intervalu pokrytí, blížícího se 100%, je třeba rozšířit standardní nejistotu koeficientem rozšíření  , jehož význam je v podstatě shodný s významem kvantilů u normálního Gaussova rozdělení, kde  =2 pro rozšíření na 95% a  =3 pro rozšíření na 99,7% pravděpodobnosti apod. rozšířená nejistota je pak vyjádřena vztahem

(1.45)

kde

je rozšířená nejistota

 

koeficient rozšíření

 

standardní nejistota.
Zdroje nejistot

       Jako zdroje nejistot lze označit veškeré jevy, které nějakým způsobem mohou ovlivnit neurčitost jednoznačného stanovení výsledku měření a tím vzdalují naměřenou hodnotu od hodnoty skutečné. Značnou roli sehrává také skutečnost, zda jde o měřicí metody přímé nebo nepřímé. Na nejistoty působí výběr měřicích přístrojů analogových nebo číslicových, použití různých filtrů. Vzorkovačů a dalších prostředků v celé trase přenosu a úpravy měřicího signálu. K nejistotám velmi výrazně přispívají rušivé vlivy prostředí v tom nejširším smyslu slova.

       Nejčastější zdroje nejistot:

-

Nedokonalá či neúplná definice měřené veličiny nebo její realizace

-

Nevhodný výběr přístroje (rozlišovací schopnost aj.)

-

nevhodný (nereprezentativní) výběr vzorků měření

-

nevhodný postup při měření

-

zjednodušení (zaokrouhlení) konstant a převzatých hodnot

-

linearizace, aproximace, interpolace a nebo extrapolace při vyhodnocení

-

neznámé nebo nekompenzované vlivy prostředí

-

nedodržení shodných podmínek při opakovaných měřeních

-

subjektivní vliv obsluhy

-

nepřesnot etalonů a referenčních materiálů

       Některé ze zdrojů se projevují výhradně či výrazněji v nejistotách vyhodnocovaných metodou A, jiné při použití metody typu B. Mnohé zdroje ale mohou být příčinou obou skupin nejistot, a zde právě číhá největší nebezpečí v podobě opomenutí jedné ze složek, což může mít i velmi výrazný zkreslující účinek.