V úvodu hned zdůrazňuji, že Booleova algebra není algebrou čísel, s jakou se setkáváme v matematice. Je to algebra stavu. Vzhledem ke klasické algebře, je proto jinak definovaná, např. v ni vůbec neexistují operace odčítání a děleni.
Základní funkce Booleovy algebry jsou:
Tyto tři funkce si nyní podrobně popíšeme. Proměnné budeme označovat velkými písmeny bez indexu.
Rovněž oba logické stavy, logickou jedničku a nulu budeme zapisovat symboly 1, 0. Pro operace logického součtu a součinu budeme používat symboly ( +) a ( . ).
Logický součet ( OR ):
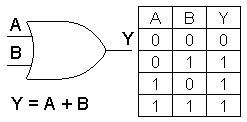
Výstup proměnná Y má hodnotu 1 tehdy, má-li alespoň jedna ze vstupních proměnných hodnotu 1.
Logický součin ( AND ):
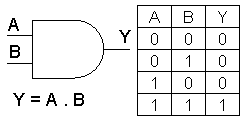
Výstup proměnná Y má hodnotu 1 tehdy, má-li hodnotu 1 obě vstupní proměnné.
Negace:
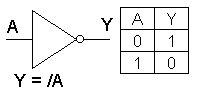
Výstupní proměnna Y má vždy opačnou hodnotu než vstupní proměnná.
Uvedené tři základní funkce lze rozšířit na libovolný počet vstupních proměnných a to v přímém i inverzním tvaru. Kombinaci takových funkcí pak vznikají obecné logické rovnice pro N proměnných. Uveďme si nyní některá pravidla pro práci s Booleovou algebrou. Jsou většinou formálně shodná s pravidly vžité s číselnou algebrou. Přesto pozorujeme ( nebo si spíše většinou neuvědomujeme) některé odchylky, vyplývající z omezení, že máme k dispozice dvě hodnoty a to 1 a 0.
Zcela logická jsou pravidla pro součet a součin jedné proměnné s konstantou. Tyto i ostatní vztahy si lze ověřit dosazením hodnot 1 a 0 za proměnnou. Již při dvou proměnných vidíme, jaký takový důkaz je zdlouhavý (Postupné vyčerpaní všech možností.).
| A + 0 = A | --- UKÁZKA SIMULACE |
| A + 1 = 1 | |
| A + A = A | |
| A + /A = 1 | |
| A . 0 = 0 | --- UKÁZKA SIMULACE |
| A . 1 = A | |
| A . A = A | |
| A . /A = 0 |
Pravidla pro operace s několika proměnnýma se řídí podobnými zákony, jaké známe. Jsou uvedené společně pro logický součet a součin.
A + B = B + A
A . B = B . A
(A + B) + C = A + (B + C)
(A . B) . C = A . (B . C)
Distributivní zákony:
(A + B ) . C = A . C + B . C
(A + C) . (B + C) = A.B + C
Od definice číselné algebry se však jeden z nich zcela odlišuje. Je to druhý z distributivních zákonů (pro násobení). Vysvětlíme si to v následujícím přikladu:
(A + C) . (B + C) = A.B + B.C + A.C + C
Podle prvního distributivního zákona pro sčítání upravíme rovnici do tvaru (A + C) . (B + C) = A.B + (A + B) C + C v němž výraz (A + B) C muže při A + B = 0, popř. 1 nabývat hodnoty (A + B) . C = 0, popř. C. Proto platí, že A.B + 0 (popř. C) + C = A.B + C a lze psát rovnost (A + C) . (B + C) = A.B + C, shodnou s definicí 2. distributivního zákona.
Dokazovat obdobným způsobem správnost tohoto zákona při konverzi v opačném směru by bylo obtížnější.
//A = A
Po dvojnásobné negaci je výstupní proměnná totožná se vstupní proměnnou.
/(A
. B) = /A + /B /(A + B) = /A . /BDe Morganovy zákony:
Zcela mimořádnou vlastností Booleovy algebry je její dualita. Vyplývá z naprosté symetrie základních zákonu. Ke každému zákonu lze vždy najít zákon další, k původnímu duální. Duální zákon lze přitom odvodit z původního poměrně jednoduchým postupem, založeným na využití principu inverze funkce. Důsledkem duality je to, že libovolnou logickou funkci můžeme volbou vhodného postupu vyjádřit v jiném (duálním) tvaru. Které zákony jsou vzájemně duální?
Disjunktní a konjunktní funkce jedné proměnné, stejně jako první a druhý komutativní, asociativní a distributivní zákon. Vzájemně duální zákony lze použít k tomu, abychom libovolný logický výraz vyjádřili v jeho duálním tvaru. Přitom je nutné postupovat podle určitých pravidel, v nichž klíčovou roli hraje již zmíněný princip inverze logické funkce. Zvládnutí těchto pravidel, formulovaných de Morganovými zákony a v zobecněné formě Shannovým teorémem, je velmi užitečné, protože na nich založených postup odvození duálního logického výrazu nevyžaduje důkazu. Proti intuitivnímu přístupu ke konkrétním úlohám, které většinou zdaleka nemají jediné řešení, se tak práce velmi zjednodušuje a omezuje se možnost zavádění chyb do výpočtu, zvláště při větším počtu proměnných.