LOGICKÉ OBVODYLOGICKÉ OBVODYElektronické obvody, které realizují logické funkce dělíme do základních dvou skupin: na tzv. kombinační a sekvenční logické systémy. První skupina (logická hradla) je charakterizována tím, že výstupní stav systému závisí pouze na okamžitých stavech (kombinaci) vstupních logických proměnných; při jejich změně dochází ke změně výstupního stavu se zpožděním, daném jen dobou průchodu signálu přes použité elektronické obvody. Sekvenční logické systémy (systémy s mezipamětí, klopné obvody) generují výstupní stav na základě hodnoty vstupních logických proměnných a na základě předchozí hodnoty výstupu. Výstup těchto obvodů je tedy definován jen tehdy, je-li definována časová posloupnost (sekvence) změn vstupních hodnot; z toho též plyne jejich název. Probereme nejprve příklady kombinačních a pak sekvenčních logických systémů.
Je to takový logický obvod, jehož vektor výstupní proměnných závisí pouze na hodnotách vektoru vstupních proměnných. Výstupní proměnné tedy nezávisí na stavu obvodu, pokud neuvažujeme přechodný režim.
Kombinujeme-li hradla OR a AND, s invertorem, můžeme vytvořit celou řadu dalších logických funkcí, z nichž nejpoužívanější jsou NAND - tzv. Shefferova funkce a NOR - tzv. Pierceova funkce. Vytvoří se tak, že na výstup hradla AND event. OR připojíme invertor. Výsledné pravdivostní tabulky pak jsou:
| A | B | /(A.B) |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| A | B | /(A+B) |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Podle de Morganových zákonů bychom mohli vytvořit hradlo NAND připojením dvou invertorů na oba vstupy hradla OR:
Obdobně hradlo NOR lze vytvořit z hradla AND a dvou invertorů na vstupech:
Funkce NAND a NOR lze rozšířit na libovolný počet vstupních logických proměnných. Definice těchto funkcí si čtenář jistě snadno utvoří sám.
Všimneme si ještě tří složených logických funkcí, které pro svou důležitost jsou často realizovány jako jeden logický člen. Jsou to funkce EXCLUSIVE-OR nazývaná též neekvivalence, funkce EXCLUSIVE-NOR neboli ekvivalence, shodnost a funkce čtyř logických proměnných AND - NOR, zvaná také AND - OR - INVERT.
Funkci EXCLUSIVE - OR lze obecně definovat pro n logických proměnných. Tato funkce nabývá hodnoty 1 právě když existuje mezi n vstupními logickými proměnnými alespoň jedna, která má jinou hodnotu, než ostatní. Lze snadno dokázat (důkaz je přenechán čtenáři), že vyjádřena v Booleově algebře bude funkce EXCLUSIVE - OR mít tvar (A1,A2, ..., An jsou vstupní logické proměnné):
Zde jsme si rovněž zavedli značku pro označení této logické funkce. Aby nedošlo k záměně se značkou logického součtu, budeme v těchto skriptech užívat pro logický součet a součin pouze značek “ +” a “ .”.
Nyní si podrobněji rozebereme hradlo EXCLUSIVE-OR pro dvě vstupní logické proměnné. Je zřejmé, že rozšíření pro více logických proměnných by šlo provést např. tímto způsobem:
neboť
existuje-li alespoň jedna proměnná Ai pro kterou platí
pro i =
1, 2, 3, ..., n-1, je součet na pravé straně tohoto výrazu roven logické 1
nezávisle na hodnotách ostatních sčítanců. Můžeme tedy vytvořit funkci
EXCLUSIVE-OR pro n proměnných pomocí hradel realizujících tuto funkci pro
dvě logické proměnné a hradel základních. Jsou-li A, B vstupní
logické proměnné, lze tuto funkci zapsat jako:
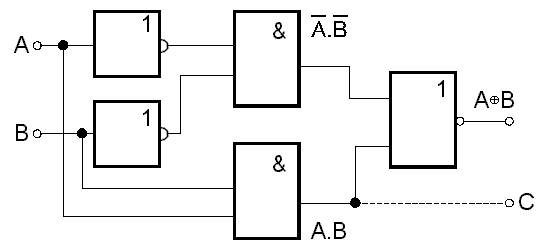
| A | B | A Å B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Při řešení kombinačních logických obvodů postupujeme následovně:
- zapíšeme stavy vstupních a výstupních proměnných
- provedeme minimalizaci ( pomocí algebry, nebo Karnaughovy mapy )
- vypíšeme zjednodušenou funkci
- sestavíme obvod pomocí hradel
Jsou to obvody jejichž výstupní hodnota závisí na historii hodnot vstupního vektoru a vnitřních veličinách.
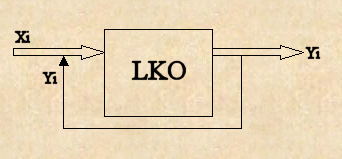
Řada logických sítí pracuje v synchronismu s posloupností impulsů, které jsou generovány zvláštním generátorem, který není součástí této sítě. Změna stavu výstupu takové logické sítě pak závisí jednak na stavu vstupů sítě při přítomnosti impulsu, jednak může záviset na historii vstupů, tj. na jejich stavech při přítomnosti dřívějších impulsů. Takovýmto obvodům říkáme sekvenční logické systémy a řídící impulsy nazýváme hodinovými impulsy. Obvody řízené hodinovým signálem se také nazývají synchronní. Sled operací v jednom kroku se děje po přijetí hodinového (synchronizačního) signálu. Naopak obvody asynchronnní nepracují v závislosti na hodinovém (synchronizačním) impulsu. Je zřejmé,že sekvenční obvody musí obsahovat prvky, které jsou schopny si pamatovat informace minimálně po dobu mezi dvěma hodinovými impulsy.
Postup při realizaci sekvenčního logického obvodu je obdobný jako u kombinačního logického obvodu. Zadání bývají většinou ústní a řešitel musí stanovit zpětnou vazbu mezi výstupní a vstupní veličinou.
Např: Regulace teploty v mezích, pomocí topné spirály. Máme dvě vstupní veličiny max (maximální teplota) a min (minimální teplota). Sepnutí topné spirály tedy nezávisí jen na dosažení hladiny max, min ale také na předchozím stavu obvodu.
Mezi sekvenční obvody se řadí i paměťové členy. Souhrnně nazývané Klopné obvody.
Klopné obvody se díky své schopnosti pamatovat si předchozí stav označují také jako paměťové členy.
Schématická značka:
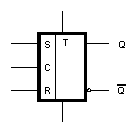
Základním obvodem, který je schopen setrvat v určitém stavu (logické 0 nebo 1) bez aplikace vnějších logických úrovní (mimo napájecí napětí ovšem) je tzv.paměťová buňka, neboli klopný obvod. Nejjednodušší klopný obvod vytvoříme pomocí dvou invertorů, kterým křížem propojíme vstupy a výstupy.
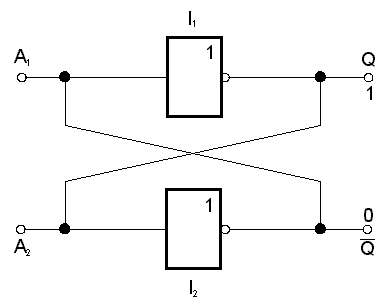
Po zapojení napájecího napětí nastaví se na výstupu jednoho invertoru logická jednička a na druhém výstupu logická nula. Tento stav je logicky konzistentní, neboť je-li např. na výstupu Q invertoru I1 logická jednička, je tato i na vstupu A2 invertoru I2, který musí mít tedy na svém výstupu /Q nulu. Nula je tedy i na vstupu A1 invertoru I1 ,což odpovídá stavu na jeho výstupu. Chceme-li do paměťové buňky “zapisovat”, tj. nastavovat výstup Q do úrovně 0 nebo 1, musíme použít místo prostých invertorů dvojvstupová hradla NAND a propojit je společně se dvěma invertory.
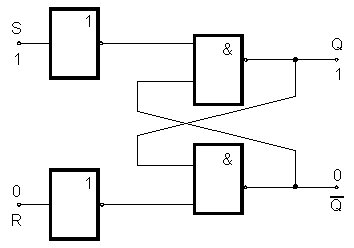
Logické úrovně pro vstupní signály S = 1, R = 0 jsou na obrázku naznačeny. V sekvenčním logickém systému je třeba, aby se nastavení nebo nulování klopných obvodů dálo v synchronismu s hodinovými impulsy. To lze zabezpečit tak, že místo invertorů, použijeme dvoustupová hradla NAND, která otevíráme hodinovými impulsy. Je zřejmé, že je-li úroveň na hodinovém vstupu log 0 (stav mezi dvěma impulsy), nezmění klopný obvod svůj stav; pamatuje si jej po dobu mezi dvěma hodinovými impulsy. Všimneme si nyní následující pravdivostní tabulky.
| Rn | Sn | Qn+1 |
| 0 | 0 | Qn |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | ? |
Jsou-li vstupy R a S uzemněny (je-li na nich logická nula), pak na výstupech řídících hradel je logická jednička nezávisle na úrovni hodinového vstupu. Výstupy Q a /Q zůstávají proto na úrovni, do které se dostaly před tím, než jsme na oba vstupy R a S logickou nulu přivedli. Přivedením logické nuly na oba vstupy R i S zablokujeme tedy stav výstupů Q a /Q, které jsou nyní nezávislé na hodinových impulsech.
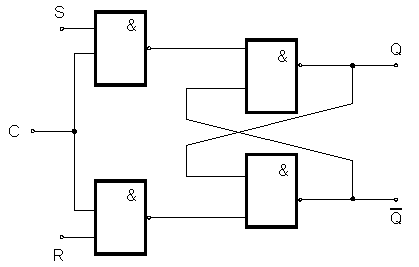
Předpokládejme nyní, že Sn = 1, Rn = 0. Po příchodu hodinového impulsu je pak na výstupu hradla A3 logická 0 a na výstupu hradla A4 logická jednička. Prostudujeme-li logické úrovně zapojení uvidíme, že obvod nastavíme do stavu, kdy Q = 1 a /Q = 0. Tento stav setrvává do té doby, dokud v době příchodu hodinového impulsu je na vstupech S = 1 a R = 0. Ze symetrie obvodu okamžitě plyne, že pro Sn = 0 a Rn = 1, nastavíme obvod po příchodu hodinového impulsu do stavu Q = 0 a /Q= 1.
Je-li
Sn = 1 = Rn, nastaví se výstupy hradel A3 a A4
po příchodu hodinového impulsu do stavu logické nuly. Tento stav by opět
implikoval, že oba výstupy hradel A1 a A2 by měly být
ve stavu logické jedničky, což je neslučitelné se zapojením klopného
obvodu. Ve skutečnosti se
stane to, že v závislosti na tom, který z výstupů hradel A3
a A4 stoupá
po ukončení hodinového
impulsu rychleji, nastaví se na výstupech /Q a Q buď stav Q = 1 nebo Q = 0.
Stav výstupů proto nezáleží ani na stavech vstupů ani na úrovni hodinového
impulsu, ale na vnitřních parametrech obvodu; je to tedy neurčitý stav a v
tabulce je znázorněn otazníkem. Proto se při buzení tohoto klopného obvodu
musí pamatovat na to, aby stav Rn = Sn = 1 nemohl nastat.
Kromě právě
popsaného klopného obvodu R-S jsou používány tři další typy klopných
obvodů: dvojčinné klopné obvody J-K, T a D. Dvojčinné klopné obvody J-K,
D a T odstraňují neurčitý stav obvodu R-S. Obvod T pracuje jako binární
obvod, který mění svůj stav po každém hodinovém impulsu Qn+1=
/Qn.
Schématická značka:
Pro odstranění neurčitého stavu klopného obvodu R-S byl vyvinut tzv. dvojčinný klopný obvod J-K. Principiální zapojení je na obrázku níže.
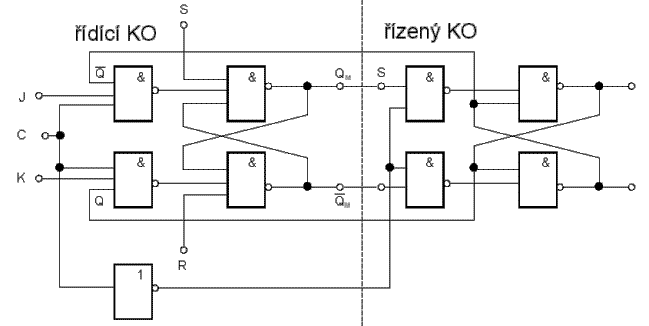
Zapojení obsahuje dva řízené klopné obvody R-S, u nichž výstupy Q a /Q
prvního jsou navázány na vstupy S a R (po řadě) druhého. Druhý klopný
obvod se řídí invertovanými hodinovými impulsy a zpětná vazba je vedena z
výstupu druhého klopného obvodu na vstup prvního. První klopný obvod se
nazývá řídicí (master), druhý klopný obvod je řízený (slave). S náběžnou
hranou hodinového impulsu se nastavuje úroveň na výstupech řídícího
obvodu; řízený obvod je uzavřen, neboť úroveň na jeho hodinovém vstupu
/C = 0. S úběžnou hranou hodinového impulsu se uzavírá vstup řídícího
klopného obvodu a stav na jeho výstupu je kopírován řízeným klopným
obvodem. Jeho výstupní úrovně jsou vedeny zpětnou vazbou na vstup řídícího
obvodu, tam však nezpůsobí žádnou změnu, neboť tentokrát je řídící
obvod uzavřen (C = 0). Asynchronní vstupy jsou zavedeny do řídicího klopného
obvodu. Nastavíme-li asynchronními vstupy řídící klopný obvod, přesune
se tato informace do řízeného klopného obvodu okamžitě (je-li C = 0), neboť
mezi hodinovými impulsy je C = 0, tedy /C = 1; řízený klopný obvod, ovládaný
signálem /C, je tedy otevřen.
Vznikne z obvodu typu J-K, vložíme-li invertor mezi vstupy J a K tak, že K je komplementem J. Z pravdivostní tabulky obvodu J - K plyne, že Qn+1 = 1 pro Dn = Jn = /Kn = 1 a Qn+1 = 0 pro Dn = Jn = /Kn = 0. Tedy Qn+1 = Dn. Vzhledem k tomu, že pravdivostní tabulka obvodu J-K pro J =/K se neliší od tabulky obvodu R-S pro R =/S, můžeme obvod tohoto typu rovněž sestavit z řízeného obvodu R-S (v tom případě hovoříme o jednoduchém nebo jednočinném klopném obvodu). Takový obvod mění svůj stav při náběžné hraně hodinového impulsu; v případě, že D obvod sestavíme z obvodu J-K typu master - slave, mění se stav s týlovou hranou hodinového impulsu. Klopné obvody typu D mohou sloužit jako paměti binární informace, která se vybaví hodinovým impulsem k dalšímu zpracování. Příkladem jednoduchého obvodu typu D je integrovaný obvod 7474 (dva jednoduché D-obvody v jednom pouzdru).
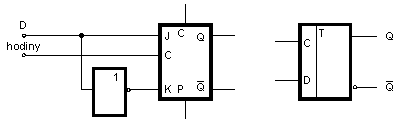
Mění svůj stav při každém hodinovém impulsu. Je tedy Qn+1 = /Qn. Z pravdivostní tabulky obvodu J-K můžeme vidět, že tuto funkci plní obvod J-K pro J = K = 1. Obvod typu T má tedy dva vstupy - vstup T (spojené vstupy J-K) a vstup pro hodinové impulsy. Je-li T = 1 , obvod se překlápí, Qn+1 = /Qn, je-li T = 0, obvod zůstává překlopen do původního stavu; Qn+1 = Qn. Tato funkce obvodu T je využita v synchronníoh čítačích - viz níže. Pokud nepotřebujeme obvod T elektricky ovládat, vystačíme s obvodem typu D , u něhož spojíme výstup /Qse vstupem D. Snadno nahlédneme, že je pak Qn+1 = /Qn.
Při aplikacích jsou důležité čtyři typy klopných obvodů: klopný obvod R-S (resp. řízený klopný obvod R-S), klopný obvod J-K, D a T. Obvody typu J-K a D jsou vyráběny v integrované formě v různých stupních integrace, obvod typu R-S je možné sestrojit pomocí hradel NAND nebo použít místo něj obvod J-K. Rovněž obvod typu T se dá snadno vytvořit z obvodu typu J-K event. z obvodu typu D. Klopné obvody mívají kromě synchronních vstupů dat ještě tzv. přímé neboli asynchronní vstupy, jimiž je možno nastavovat výstupy klopného obvodu do stavu Q = 1 nebo Q = 0 v době mezi dvěma hodinovými impulsy. Je-li klopný obvod typu master-slave, mění svůj stav při týlové hraně hodinového impulsu; jinak při náběžné hraně. Níže uvedená tabulka znázorňuje přehledně pravdivostní tabulky jednotlivých klopných obvodů, v dalších odstavcích jsou uvedeny jejich nejčastější aplikace.
| R-S | J-K | D | T | asynchronní vstupy | |||||||||
| Sn | Rn | Qn+1 | Jn | Kn | Qn+1 | Dn | Qn+1 | Tn | Qn+1 | C | R | S | Q |
| 0 | 0 | Qn | 0 | 0 | Qn | 1 | 1 | 1 | Qn | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | /Qn | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | * | ||||
| 1 | 1 | ? | 1 | 1 | /Qn | ||||||||