Logická funkce vyjádřená úplnou základní součtovou nebo součinovou formou z pravdivostní tabulky není jediným možným vyjádřením realizováné logické funkce. Většinou lze nalézt jednodušší algebraické vyjádření, které povede ke snížení počti operací a tedy menší složitosti obvodu. Výsledkem této činnosti je tedy nalezení minimálního výrazu, t.j. výrazu který má nejmenší četnost všech vyskytujících se proměnných. Četnost proměnných je v tomto případě dána prostým algebraickým součtem proměnných vyskytujících se ve výrazu bez ohledu na jejich index, a bez ohledu na to zda proměnné jsou přímé nebo negované. Pojem minimálnosti lze definovat i z jiných hledisek, např. počtu operací, součástkové základny, doby zpoždění, atd. K minimalizaci logické funkce vyjádřené pomocí logického výrazu se nejčastěji používá:
Obecný postup se dá charakterizovat následujícím způsobem:
Při provádění úprav logických výrazů můžeme s výhodou využít tabulky, kde jsou uvedeny nejdůležitější identity platné obecně v Booleových algebrách.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
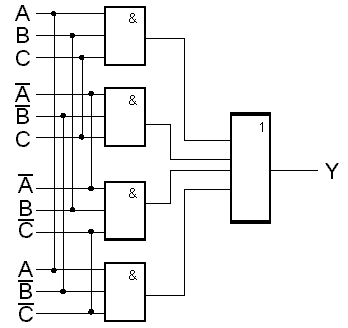
Nejprve si vysvětlíme, jakým způsobem si sestavíme logický výraz, je-li dána pravdivostní tabulka. Obecně totiž může být logická funkce zadána tabulkou, popisem nebo zapojením logických členů. Je-li logická funkce zadána popisem, snadno sestrojíme z popisu pravdivostní tabulku nebo přímo Booleovský výraz. Pokud bychom vycházeli z daného zapojení logické sítě, není jistě složité odvodit logický výraz ze zapojení. Pokud máme pravdivostní tabulku, překreslíme ji nejprve tak, aby obsahovala jak vstupní proměnné, tak jejich komplementy. Pak si všímáme jen řádků, ve kterých má výsledek nabýt logické jedničky a napíšeme součin všech vstupních proměnných nebo jejich komplementů, které nabývají v tomtéž řádku hodnoty 1. Tento postup opakujeme pro všechny řádky, pro které je výstup roven 1. Například pro 3 vstupní logické proměnné máme dánu tabulku vlevo:
Tu přepíšeme užitím rovněž negovaných vstupních proměnných (vpravo):
| A | B | C | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| A | /A | B | /B | C | /C | Y |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 |
![]()
Nyní uplatníme své znalosti identit platných Booleově algebře. Na výraz
![]()
uplatníme zákon komutativní
![]()
vytkneme C event.
![]()
![]()
a použijeme identity
![]()
Substituce
![]() ,
, ![]()
zjednoduší výraz na
![]()
Použitím definice funkce EXCLUSIVE-OR získáme nakonec
![]()
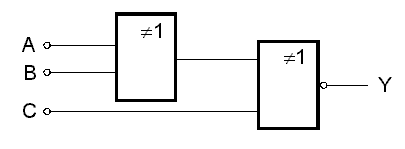
Funkci Y tedy reprezentují dvě hradla EXCLUSIVE-OR zapojená v kaskádě jak je ukázáno na obrázku níže. Funkce Y je též příkladem kombinačního logického systému.
Způsob sestavení mapy zajišťuje určité kódování proměnných (Grayův kód), čímž je docíleno toho, že sousední čtverečky se v mapě liší v jedné proměnné. Tuto podmínku splňují i čtverečky krajních řádků a sloupců. Princip zjednodušení spočívá v grafickém sloučení sousedních čtverců a jejich popsání pomocí vstupních proměnných. Grafický postup v podstatě odstraňuje méně přehledné zápisy dílčích součtů nebo součinů.
Zjednodušte funkci F(x3,x2,x1,x0) = CD33H
Pro danou funkci je pravdivostní tabulka následující.
| x3 | x2 | x1 | x0 | Y |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Karnaughova mapa funkce F
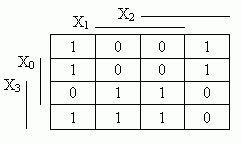
smyčkou označíme sousední čtverečky, v nichž funkce nabývá hodnot logické jedničky. Tyto smyčky vypíšeme jako dílčí součty.
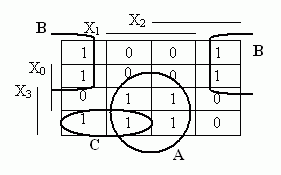
Dílčí součin označený smyčkou A bychom popsaly takto :
A = x3/x2x1x0 + x3x2x1x0 + x3/x2x1/x0 + x3x2x1/x0 = x3x2x1(/x2 + x2) + x3x2x1(/x2 + x2) = x3x2(/x0 + x0) = x3x1
pro smyčku B a C lze z mapy přímo psát:
B = /x2/x1, C = /x2x2/x0
Výsledná funkce má má potom tvar:
F = A + B + C = x3x1 + /x2/x1 + /x2x2/x0
smyčkou označíme sousední čtverečky, v nichž funkce nabývá hodnot logické 0 a tyto smyčky vypíšeme jako dílčí součty.
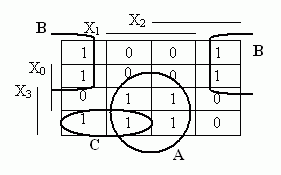
Pro jednotlivé smyčky platí:
A = x3 + /x1 B = x3 + x2 + /x1 C = /x3 + x1 + / x0
Výslednou funkci dostaneme jako součin dílčích součtů.
F = A . B . C = (x3 + / x1) . (x3 + x2 + / x1) . (/x3 + x1 + / x0)
Z Logických výrazů je vidět, že zjednodušené výrazy jsou shodné a oba tvary tedy ekvivalentní. Minimalizace logické funkce pomocí Karnaughovy mapy se vykonává na základě následujících pravidel:
- musí být pokryty všechny čtverečky, v nichž funkce nabývá hodnot log 1 ( pro součtový tvar ) a log 0 ( pro součinový tvar ).
- smyčka musí zahrnovat 2n sousedních čtverečků, ( kde n = 0, 1, 2, 3, ... )
- snažíme se dosáhnout minimálního počtu smyček ( minimální počet dílčích součinů nebo součtů ).
- snažíme se dosáhnout minimálního počtu proměnných v jednotlivých součinech nebo součtech.
Tímto se z daného součinu, resp. součtu vyloučí proměnná, která mění svůj stav
V případě neúplné funkce je postup stejný, pouze nedefinované hodnotě se ve vytvořené smyčce přiřadí konkrétní hodnota log 1 nebo log 0.