Každý matematický zápis funkce se ve své podstatě vyznačuje svojí jednoznačností. Protože však pro zápis logických funkcí nelze použít známe způsoby z matematiky, zapisují se jiným jednoznačným způsobem.
Zápis pomocí pravdivostní tabulky je nejznámější způsob zápisu. Tabulka pro úplnou logickou funkci obsahuje pro n vstupních proměnných 2n kombinací logických hodnot a proto musí mít 2n řádků. J zřejmé že tento zápis je vhodný pro menší počet vstupních proměnných. Například pro 8 vstupních proměnných vychází až 256 řádků a takový zápis vzhledem ke svým rozměrům ztrácí na přehlednosti. Pro snížení počtu řádků se proto někdy používá tzv. zhuštěný zápis. Princip zhuštěného zápisu spočívá v použití symbolu X i pro hodnoty vstupních proměnných. V našem případě symbol X znamená, že logická hodnota výstupní proměnné je stejná pro logickou hodnotu dané vstupní proměnné 0 nebo 1. Princip zhuštěného zápisu je zřejmý z následující tabulky.
Zapsaná funkce obsahuje tři vstupní proměnné A, B, C a jednu výstupní proměnnou Y. Ke každé kombinaci vstupních proměnných je přiřazena hodnota výstupní proměnné. Je tedy zřejmá závislost výstupní proměnné na proměnných vstupních. Počet kombinací vstupních proměnných je závislý na jejich počtu a vypočítá se ze vzorce 2n , kde n je počet vstupních proměnných.
| A | B | C | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| A | B | C | Y |
| 0 | X | 0 | 0 |
| 0 | X | 1 | 1 |
| 1 | X | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 |
Logická funkce využívá skutečnosti, že logické hodnoty se ztotožňují s číselnou hodnotou. Logická hodnota 1 se ztotožní s číselnou hodnotou 1, logická hodnota 0 se ztotožní s číselnou hodnotou 0. Na základě záměny logické hodnoty za číselnou lze vstupní n-tici chápat jako číslo vyjádřené ve dvojkové soustavě. Takové číslo se potom nazývá index. Předpokladem využití číselného zápisu však je pevně definované pořadí vstupních proměnných. Toto pořadí se uvádí v závorce za symbolem funkce, přičemž zároveň vyjadřuje i váhové pořadí proměnných, zleva doprava, od nejvyšší váhy k váze nejnižší. Například n-tice x2,x1,x0 = 0I0 = 0102 = 210
Existují dvě základní formy zápisu, disjunktivní a konjunktivní. V disjunktivním číselném zápisu se za symbolem rovnosti uvádí symbol D a v závorce jsou potom uvedeny indexy vstupní n-tice, vyjádřené v desítkové soustavě, v nichž logická funkce nabývá hodnoty logické I. U konjunktivního číselného zápisu je za symbolem rovnosti uvedeno K a v závorce jsou uvedeny indexy v nichž logická funkce nabývá hodnoty 0.
f(x2,x1,x0) = D(1, 3, 4, 6)
f(x2,x1,x0) = K(0, 2, 5, 7)
Neúplnou logickou funkci nelze tímto způsobem zapsat
Tento zápis logické funkce využívá skutečnosti, že logické hodnoty funkce jsou uspořádány v řádcích a uvažují se jako hodnoty číselné. Pořadí vstupních proměnných je uvedeno v závorce za symbolem funkce a určuje váhu proměnné. První hodnota za symbolem rovnosti odpovídá nejvyššímu indexu a poslední hodnota nejnižšího indexu vstupní n-tice. Hodnoty logické funkce jsou rovněž psány sestupně zleva doprava. Vektorový zápis logické funkce lze psát ve tvaru:
f(x2,x1,x0) = 01111010.
Protože funkční hodnota v tomto případě představuje číslo ve dvojkové soustavě, lze tento zápis modifikovat i do jiných číselných soustav.
f(x2,x1,x0) = 011110102
f(x2,x1,x0) = 1728
f(x2,x1,x0) = 7AH
Je to geometrické znázornění definičního oboru {0, I}n logické funkce v rovině pomocí čtverců, přičemž každé n-tici oboru je použitým kódováním přiřazen čtverec. Mapa tedy tvoří síť obsahující 2n čtverců. Příklad mapy pro n = 4 a způsob přiřazení čtverců jednotlivým čtveřicím hodnot x3, x2, x1, x0. Způsob kódování je zřejmý z obrázku níže.
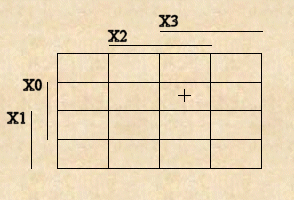
Pomocí kódovacích čar na levém a horním okraji mapy a dle připsaných proměnných jsou definovány čtverce, ve kterých jednotlivé vstupní proměnné nabývají hodnoty logické 0 a I. Předpokládá se, že v oblasti nacházející se pod čarou příslušné proměnné tato proměnná nabývá hodnot I a mimo tuto oblast hodnotu O. Čtverec označený + proto odpovídá vstupní n-tici II0I. Takto uspořádaná mapa se nazývá Karnaughova mapa.
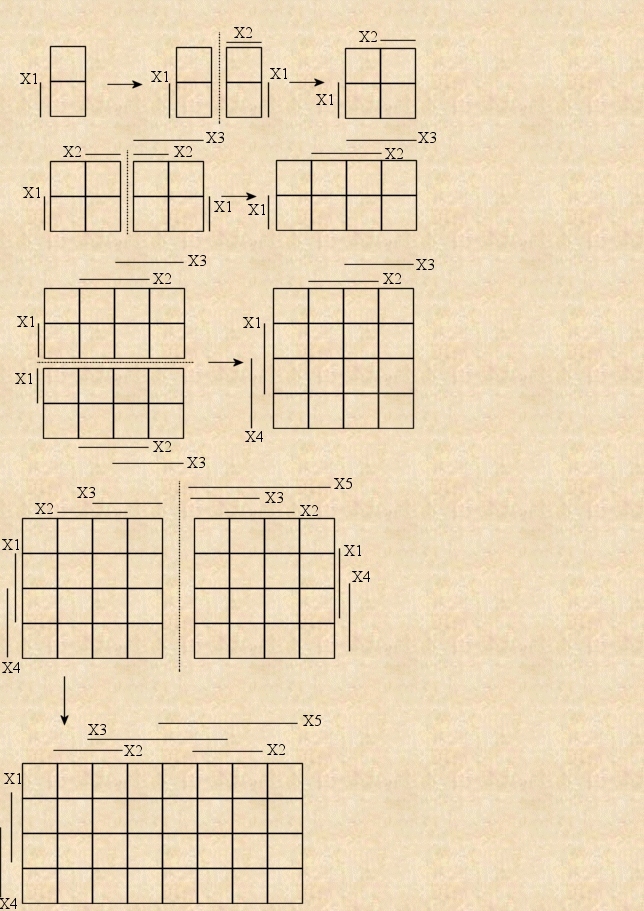
Postup vytvoření Karnaughovy mapy pro libovolný počet proměnných a zajištění správného kódování vychází z mapy pro jednu proměnnou a je uveden na obrázku níže. Algoritmus vytvoření mapy pro n+1 proměnných vychází z mapy pro n proměnných a spočívá ve vytvoření zrcadlového obrazu mapy a jeho připojení k původní mapě. Nový zrcadlový obraz se označí novou proměnnou. Z hlediska přehledu a orientace se používají mapy nejvíce pro 5 proměnných.