Měření hmotnosti pomocí tenzometrů (Vyhodnocení chyb)
Tato úloha se zabývá vyhodnocením dat a určením náhodných chyb jednotlivých odečtů měření.
Zadání
- Zkalibrujte celý měřicí systém včetně celého měřicího řetězce.
- Proveďte měření pro 3 konstantní hodnoty hmotnosti (soubor 30 hodnot).
- Určete náhodné chyby jednotlivých odečtů a aritmetického průměru pro soubor 10, 20 a 30 měření a porovnejte jejich velikosti.
- Sestrojte empirickou křivku četnosti chyb pro daný soubor měření a vyhodnoťte jejich průběh.
Schéma zapojení
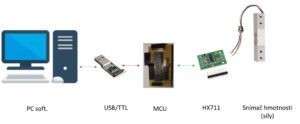
Obr. 1 Blokové schéma zapojení – řetězec
Teoretický rozbor
- Náhodné chyby (chyby stálosti) jednotlivých měření nebo aritmetického průměru je možno určit jen z většího počtu měření statistickými metodami. Již samým výpočtem aritmetického průměru ze souboru n měření se přibližujeme ke skutečné hodnotě měřené veličiny. Hovoříme o tom, že aritmetický průměr x¯ je nejlepším odhadem skutečné hodnoty měřené veličiny xS :
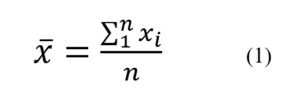
Při praktických výpočtech volíme obyčejně počet měření dosti malý, např. n = 10 či dokonce n = 5. Gaussův (normální) zákon rozdělení náhodných chyb předpokládá, že relativní četnost neboli hustota pravděpodobnosti chyby je vyjádřena vztahem:
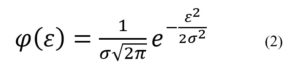
Kde  je střední kvadratická odchylka.
je střední kvadratická odchylka.
Průběh φ(ε) je znázorněn na Obr. 2.
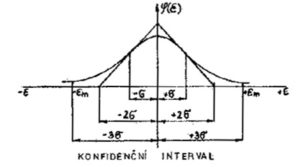
| Obr. 2 Normální Gaussův zákon rozdělení náhodných chyb |
Pro počet měření – tak jak to v praxi často bývá, můžeme střední kvadratickou odchylku pouze odhadnout. Odhad chyby jednoho měření Sx lze pak vyjádřit vztahem:

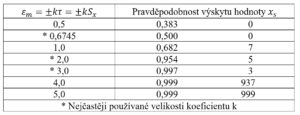
Protože se teoreticky mohou vyskytnout i chyby poměrně velké (ovšem se značně malou pravděpodobností), je možno odhad chyby měření popsat rovněž pravděpodobností, s jakou se vyskytne větší skutečná chyba v poměru k chybám menším, než je chyba vypočtená. Vztah mezi rozpětím konfidenčního intervalu (tj. k-násobkem střední kvadratické odchylky σ ) a pravděpodobností, že skutečná hodnota xS bude v mezích tohoto intervalu, je zřejmý z následující tabulky 1.
V praxi volíme velikost konfidenčního intervalu a tím i součinitel k = 3, to znamená, že mezní (maximální) náhodná chyba , takže pravděpodobnost, že skutečná hodnota měřené veličiny xs se nachází v intervalu ±3SX je 99,73%, což je hodnota dostatečně velká. Odhad chyby jednotlivých měření SX je předpokládaná chyba každého jednotlivého odečtu (bez ohledu na skutečně provedenou chybu) a počítá se proto, abychom věděli, s jakou chybou budeme na přístroji i nadále měřit za přibližně stejných podmínek. Častěji se používá odhadu náhodné chyby aritmetického průměru která je dána vztahem 4.
Tabulka 1

Postup při sestrojení empirické křivky četnosti chyb odpovídající přibližně Gaussovu normálnímu rozložení náhodných chyb:
- Do grafu (Obr. 3) na vodorovnou osu vynášíme velikost jak kladných, tak záporných zdánlivých odchylek . Každou jednotlivou chybu vyznačíme na této ose kroužkem.
- Na svislé ose vyneseme celkový počet odchylek.
- Zvolíme vhodnou velikost intervalu I pro vodorovnou osu a nakreslíme ji na pomocný papír.
- Tímto intervalem posouváme ve vhodně malých krocích (např. 1/5 I) po vodorovné ose z jedné strany na druhou a postupně v každém místě zjistíme počet odchylek v tom intervalu I, který vyneseme na svislou osu uprostřed intervalu I, v odpovídajícím měřítku (viz příklad na Obr. 3).
- Výsledná stupňovitá křivka by pro dostatečně velký počet měření n (n > 100), dostatečně malý interval I a krok posuvu se měla blížit Gaussově křivce normálního rozdělení chyb za předpokladu, že jsou vyloučeny hrubé a systematické chyby. Do takto získané křivky zakreslíme vypočtené chyby .
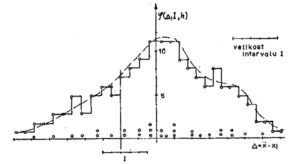
| Obr. 3 Sestrojení empirické křivky rozdělení náhodných chyb |
Postup měření
- Před vlastním měřením provedeme kalibraci měřicího systému. Senzor má lineární závislost, proto je nutno změřit min. 2 hodnoty statické charakteristiky např. při hodnotě 0 kg a 1 kg, hodnoty z převodníku překopírujeme do dvou řádků kalibrační tabulky v softwarové podpoře.
- Pro 3 vybrané hodnoty hmotnosti provedeme 30x (např. každých 5 s) měření a uložíme do souborů. Při těchto měřeních je nutno zachovat konstantní všechny okolnosti, ovlivňující měření (jeden pozorovatel provádějící odečet hodnot, kolísání otáček ventilátoru,…)
- Údaje budeme uvažovat bez systematických chyb. Z prvních desíti, prvních dvaceti a konečně ze všech třiceti odečtů se vypočte aritmetický průměr, aby bylo možno zhodnotit rozdíly změřených výsledků. Pro jednotlivé počty měření n = 10, n = 20, n = 30 vypočtěte odhad chyby aritmetického průměru dle vztahu (4). Dosažené velikosti chyb vyneste do tabulky a grafu a zhodnoťte!
- Z celkového počtu 30 měření a jejich jednotlivých odchylek [ kg ] sestrojte empirickou Gaussovu křivku výskytu chyb. Proveďte rozbor jejího průběhu, zhodnoťte vliv systematických chyb na měření, zakreslete do sestrojené křivky konfidenční intervaly odpovídající chybám.
Tabulka 2 Tabulka náhodných chyb měření tlaku

Závislosti velikosti náhodných chyb na počtu měření
Kontrolní otázky
- Uveďte postup výpočtu náhodných chyb souboru n hodnot.
- Jaký je rozdíl mezi odhadem chyby jednotlivých měření a odhadem chyby aritmetického průměru?
- Co vyjadřuje Gaussova křivka normálního rozdělení chyb, jakým je popsána vztahem?
Odpovědi k otázkám
